初中数学平行四边形的性质试题

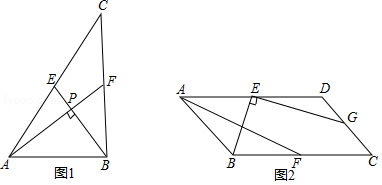
如图1， AF， BE是△ ABC的中线， AF⊥ BE，垂足为点 P，设 BC＝ a， AC＝ b， AB＝ c，则 a ²+ b ²＝5 c ²，利用这一性质计算．如图2，在▱ ABCD中， E， F， G分别是 AD， BC， CD的中点， EB⊥ EG于点 E， AD＝8， AB＝2 $\sqrt{5}$ ，则 AF＝ 　　．

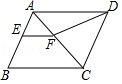
如图， P是▱ ABCD的边 AD上一点， E、 F分别是 PB、 PC的中点，若▱ ABCD的面积为16 cm ²，则△ PEF的面积（阴影部分）是 　　 cm ²．

如图，在▱ ABCD中， AC是一条对角线， EF∥ BC，且 EF与 AB相交于点 E，与 AC相交于点 F，3 AE＝2 EB，连接 DF．若 S _{△ AEF}＝1，则 S _{△ ADF}的值为 　　．

如图，在平行四边形 ABCD中， E， F分别是 AB， BC边上的中点， CE⊥ AB，垂足为 E， AF⊥ BC，垂足为 F， AF与 CE相交于点 G；

（1）求证：△ CFG≌△ AEG；

（2）若 AB＝6，求四边形 AGCD的对角线 GD的长．

如图，将平行四边形 ABCD沿对角线 BD折叠，使点 A落在点 A′处，∠1＝∠2＝48°，则∠ A′的度数为 　 　．

阅读理解：

我们知道，四边形具有不稳定性，容易变形，如图1，一个矩形发生变形后成为一个平行四边形，设这个平行四边形相邻两个内角中较小的一个内角为α，我们把 $\frac{1}{\sin \alpha }$的值叫做这个平行四边形的变形度．

（1）若矩形发生变形后的平行四边形有一个内角是120度，则这个平行四边形的变形度是　　．

猜想证明：

（2）设矩形的面积为S₁，其变形后的平行四边形面积为S₂，试猜想S₁，S₂， $\frac{1}{\sin \alpha }$之间的数量关系，并说明理由；

拓展探究：

（3）如图2，在矩形ABCD中，E是AD边上的一点，且 $A{B}^2＝\mathit{AE}•\mathit{AD}$，这个矩形发生变形后为平行四边形A₁B₁C₁D₁，E₁为E的对应点，连接B₁E₁，B₁D₁，若矩形ABCD的面积为 $4\sqrt{\pi }(m>0)$，平行四边形A₁B₁C₁D₁的面积为 $2\sqrt{\pi }(m>0)$，试求∠A₁E₁B₁+∠A₁D₁B₁的度数．

如图，在▱ABCD中， $\mathit{AB}=2\sqrt{13}\text{cm}$， $\mathit{AD}＝4\mathit{cm}，$ $\mathit{AC}\perp \mathit{BC}$，则△DBC比△ABC的周长长　　cm．

如图，A、F、B、C是半圆O上的四个点，四边形OABC是平行四边形，∠FAB＝15°，连接OF交AB于点E，过点C作OF的平行线交AB的延长线于点D，延长AF交直线CD于点H．

（1）求证：CD是半圆O的切线；

（2）若 $\mathit{DH}=6-3\sqrt{3}$，求EF和半径OA的长．

如图，在平行四边形 ABCD中， AD＞ AB．

（1）作∠ BAD的平分线交 BC于点 E，在 AD边上截取 AF＝ AB，连接 EF（要求：尺规作图，保留作图痕迹，不写作法）；

（2）判断四边形 ABEF的形状，并说明理由．

已知平行四边形 ABCD的顶点 A在第三象限，对角线 AC的中点在坐标原点，一边 AB与 x轴平行且 AB＝2，若点 A的坐标为（ a， b），则点 D的坐标为 　．

邻边不相等的平行四边形纸片，剪去一个菱形，余下的一个四边形，称为第一次操作；在余下的四边形纸片中再剪去一个菱形，又余下一个四边形，称为第二次操作；…依此类推，若第 n次操作余下的四边形是菱形，则称原平行四边形为 n阶准菱形，如图1，▱ ABCD中，若 AB＝1， BC＝2，则▱ ABCD为1阶准菱形．

（1）猜想与计算：

邻边长分别为3和5的平行四边形是 　　阶准菱形；已知▱ ABCD的邻边长分别为 a， b（ a＞ b），满足 a＝8 b+ r， b＝5 r，请写出▱ ABCD是 　　阶准菱形．

（2）操作与推理：

小明为了剪去一个菱形，进行了如下操作：如图2，把▱ ABCD沿 BE折叠（点 E在 AD上），使点 A落在 BC边上的点 F处，得到四边形 ABFE．请证明四边形 ABFE是菱形．

在▱ ABCD中， AE平分∠ BAD交边 BC于 E， DF平分∠ ADC交边 BC于 F，若 AD＝11， EF＝5，则 AB＝ 　　．

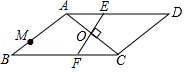
如图，在▱ ABCD中，∠ B＝30°， AB＝ AC， O是两条对角线的交点，过点 O作 AC的垂线分别交边 AD， BC于点 E， F；点 M是边 AB的一个三等分点，则△ AOE与△ BMF的面积比为 　　．

已知平行四边形 ABCD．

（1）尺规作图：作∠ BAD的平分线交直线 BC于点 E，交 DC延长线于点 F（要求：尺规作图，保留作图痕迹，不写作法）；

（2）在（1）的条件下，求证： CE＝ CF．

如图，在平行四边形 ABCD中，点 E， F， G， H分别在边 AB， BC， CD， DA上， AE＝ CG， AH＝ CF，且 EG平分∠ HEF．

（1）求证：四边形 EFGH是菱形；

（2）若 EF＝4，∠ HEF＝60°，求 EG的长．