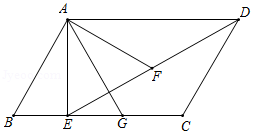
如图,在平行四边形 中, 是 边上的高,点 是 的中点, 与 关于 对称, 与 关于 对称.
(1)求证: 是等边三角形;
(2)若 ,求 的面积.
如图,在平行四边形 中, 是 上的点, ,连接 交 于点 ,则 与 的面积之比为

A. B. C. D.
如图,已知点 , 分别是平行四边形 对角线 所在直线上的两点,连接 , ,请你添加一个条件,使得 ,并证明.

如图,在 中,对角线 的垂直平分线分别交 、 于点 、 ,连接 ,若 的周长为6,则 的周长为

A.6B.12C.18D.24
如图,在 中过点 作 ,垂足为 ,连接 , 为 上一点,且 .
(1)求证: ;
(2)若 , , ,求 的长.

如图,在 中,对角线 与 交于点 ,若增加一个条件,使 成为菱形,下列给出的条件不正确的是

A. B. C. D.
如图,在 中,对角线 与 交于点 ,若增加一个条件,使 成为菱形,下列给出的条件不正确的是
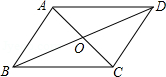
A. B. C. D.
如图,在 中, ,点 、 分别是 、 的中点.
(1)求证: ;
(2)当四边形 为菱形时,求出该菱形的面积.

如图,在 中, ,四个角的平分线 , , , 的交点分别是 , ,过点 , 分别作 与 间的垂线 与 ,在 与 上的垂足分别是 , 与 , ,连接 .
(1)求证:四边形 是矩形;
(2)已知: , , ,求 的长.

如图,已知平行四边形 中,点 为坐标原点,点 , ,函数 的图象经过点 .
(1)求 的值及直线 的函数表达式:
(2)求四边形 的周长.

四边形具有不稳定性.如图,矩形 按箭头方向变形成平行四边形 ,当变形后图形面积是原图形面积的一半时,则 .
