(·湖南株洲)某学校举行一次体育测试,从所有参加测试的学生中随机抽取10名学生的成绩,制作出如下统计表和条形统计图:
编号
|
成绩
|
等级
|
编号
|
成绩
|
等级
|
|
95
|
A
|
⑥
|
76
|
B
|
|
78
|
B
|
⑦
|
85
|
A
|
|
72
|
C
|
⑧
|
82
|
B
|
|
79
|
B
|
⑨
|
77
|
B
|
|
92
|
A
|
⑩
|
69
|
C
|
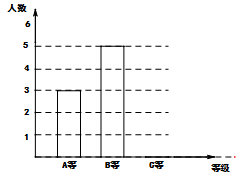
请回答下列问题:
(1)孔明同学这次测试的成绩是87分,则他的成绩等级是 ;
(2)请将条形统计图补充完整;
(3)已知该校所有参加这次测试的学生中,有60名学生成绩是A等,请根据以上抽样结果,估计该校参加这次测试的学生总人数是多少?