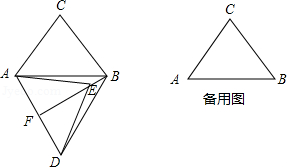
和 是两个全等的等边三角形,将它们按如图的方式放置在等边三角形 内.若求五边形 的周长,则只需知道

A. 的周长B. 的周长
C.四边形 的周长D.四边形 的周长
如图,等边 的边长为2, 的半径为1, 是 上的动点, 与 相切于 , 的最小值是

A.1B. C. D.2
如图,分别以等边三角形 的三个顶点为圆心,以边长为半径画弧,得到的封闭图形是莱洛三角形,若 ,则莱洛三角形的面积(即阴影部分面积)为

A. B. C. D.
如图,正三角形 的边长为3,将 绕它的外心 逆时针旋转 得到△ ,则它们重叠部分的面积是

A. B. C. D.
如图1,2,3分别以 的 和 为边向 外作正三角形(等边三角形)、正四边形(正方形)、正五边形, 和 相交于点 .

(1)在图1中,求证: .
(2)由(1)证得 ,由此可推得在图1中 ,请你探索在图2中, 的度数,并说明理由或写出证明过程.
(3)填空:在上述(1)(2)的基础上可得在图3中 (填写度数).
(4)由此推广到一般情形(如图4),分别以 的 和 为边向 外作正 边形, 和 仍相交于点 ,猜想得 的度数为 (用含 的式子表示).
如图,等边三角形 的边长为4,点 是 的中心, ,绕点 旋转 ,分别交线段 、 于 、 两点,连接 ,给出下列四个结论:① ;② ;③四边形 的面积始终等于 ;④ 周长的最小值为6.上述结论中正确的个数是

A.1B.2C.3D.4
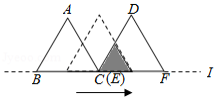
如图, 和 都是边长为2的等边三角形,它们的边 , 在同一条直线 上,点 , 重合.现将 沿着直线 向右移动,直至点 与 重合时停止移动.在此过程中,设点 移动的距离为 ,两个三角形重叠部分的面积为 ,则 随 变化的函数图象大致为
A.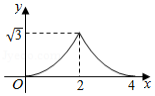
B.
C.
D.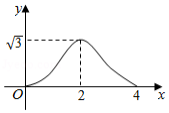
在边长为4的等边三角形 中, 为 边上的任意一点,过点 分别作 , ,垂足分别为 , ,则 .
【操作发现】
(1)如图1, 为等边三角形,先将三角板中的 角与 重合,再将三角板绕点 按顺时针方向旋转(旋转角大于 且小于 ,旋转后三角板的一直角边与 交于点 ,在三角板斜边上取一点 ,使 ,线段 上取点 ,使 ,连接 , .
①求 的度数;
② 与 相等吗?请说明理由;
【类比探究】
(2)如图2, 为等腰直角三角形, ,先将三角板的 角与 重合,再将三角板绕点 按顺时针方向旋转(旋转角大于 且小于 ,旋转后三角板的一直角边与 交于点 ,在三角板另一直角边上取一点 ,使 ,线段 上取点 ,使 ,连接 , .请直接写出探究结果:
① 的度数;
②线段 , , 之间的数量关系.
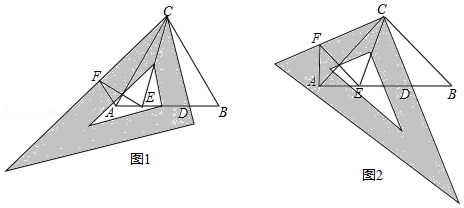
如图,面积为1的等边三角形 中, , , 分别是 , , 的中点,则 的面积是

A.1B. C. D.
如图,在平面直角坐标系中,直线 与 轴交于点 ,以 为边长作等边三角形 ,过点 作 平行于 轴,交直线 于点 ,以 为边长作等边三角形 ,过点 作 平行于 轴,交直线 于点 ,以 为边长作等边三角形 , ,则点 的横坐标是 .

【发现】如图①,已知等边 ,将直角三角板的 角顶点 任意放在 边上(点 不与点 、 重合),使两边分别交线段 、 于点 、 .
(1)若 , , ,则 ;
(2)求证: .
【思考】若将图①中的三角板的顶点 在 边上移动,保持三角板与边 、 的两个交点 、 都存在,连接 ,如图②所示,问:点 是否存在某一位置,使 平分 且 平分 ?若存在,求出 的值;若不存在,请说明理由.
【探索】如图③,在等腰 中, ,点 为 边的中点,将三角形透明纸板的一个顶点放在点 处(其中 ,使两条边分别交边 、 于点 、 (点 、 均不与 的顶点重合),连接 .设 ,则 与 的周长之比为 (用含 的表达式表示).

在 中, , ,将 绕点 按顺时针方向旋转,得到 ,旋转角为 ,点 的对应点为点 ,点 的对应点为点 ,连接 , .
(1)如图,当 时,延长 交 于点 .
①求证: 是等边三角形;
②求证: , ;
③请直接写出 的长;
(2)在旋转过程中,过点 作 垂直于直线 ,垂足为点 ,连接 ,当 ,且线段 与线段 无公共点时,请直接写出 的值.
温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.