如图,已知 , 分别为 的边 , 上两点,点 , , 在 上,点 , 在 上. 为 上一点,连接 并延长交 的延长线于点 ,交 于点 .
(1)若 为 ,请将 用含 的代数式表示;
(2)若 ,请说明当 为多少度时,直线 为 的切线;
(3)在(2)的条件下,若 ,求 的值.
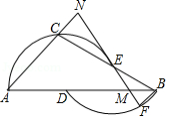
如图, 是 外接圆上的动点,且 , 位于 的两侧, ,垂足为 , 的延长线交此圆于点 . ,垂足为 , 交 于点 , , 的延长线交于点 ,且 .
(1)求证: ;
(2)设 外接圆的圆心为 ,若 , ,求 的大小.

如图1,在中,
,
,点
为
边上的动点(点
不与点
,
重合).以
为顶点作
,射线
交
边于点
,过点
作
交射线
于点
,连接
.
(1)求证:;
(2)当时(如图
,求
的长;
(3)点在
边上运动的过程中,是否存在某个位置,使得
?若存在,求出此时
的长;若不存在,请说明理由.
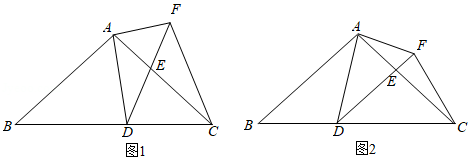
如图1,在正方形中,
平分
,交
于点
,过点
作
,交
的延长线于点
,交
的延长线于点
.
(1)求证:;
(2)如图2,连接、
,求证:
平分
;
(3)如图3,连接交
于点
,求
的值.

已知 ,以 为直径的 分别交 于 , 于 ,连接 ,若 .
(1)求证: ;
(2)若 , ,求 的长.
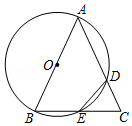
如图,已知 是 的直径,点 是圆上异于 、 的一点,连结 并延长至点 ,使 ,连结 交 于点 ,连结 .
(1)求证: 是等腰三角形;
(2)连结 并延长,与以 为切点的切线交于点 ,若 , ,求 的长.

在中,
平分
交
于点
.

(1)如图1,若,
,求
的面积;
(2)如图2,过点作
,交
的延长线于点
,分别交
,
于点
,
,且
.求证:
.
已知四边形 是 的内接四边形, 是 的直径, ,垂足为 .
(1)延长 交 于点 ,延长 , 交于点 ,如图1.求证: ;
(2)过点 作 ,垂足为 , 交 于点 ,且点 和点 都在 的左侧,如图2.若 , , ,求 的大小.

如图,在中,
,
是
边上的中点,连结
,
平分
交
于点
,过点
作
交
于点
.
(1)若,求
的度数;
(2)求证:.

如图, 已知: 是 的弦, 过点 作 交 于点 ,过点 作 的切线交 的延长线于点 ,取 的中点 ,过点 作 交 的延长线于点 ,连接 并延长交 的延长线于点 .
求证:
(1) ;
(2) .
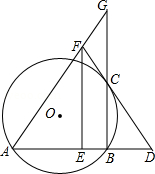
阅读下面的例题及点拨,并解决问题:
例题:如图①,在等边 中, 是 边上一点(不含端点 , , 是 的外角 的平分线上一点,且 .求证: .
点拨:如图②,作 , 与 的延长线相交于点 ,得等边 ,连接 .易证: ,可得 , ;又 ,则 ,可得 ;由 ,进一步可得 ,又因为 ,所以 ,即: .
问题:如图③,在正方形 中, 是 边上一点(不含端点 , , 是正方形 的外角 的平分线上一点,且 .求证: .

如图1,四边形 的对角线 , 相交于点 , , .
(1)过点 作 交 于点 ,求证: ;
(2)如图2,将 沿 翻折得到 .
①求证: ;
②若 ,求证: .

在菱形 中, ,点 是射线 上一动点,以 为边向右侧作等边 ,点 的位置随着点 的位置变化而变化.

(1)如图1,当点 在菱形 内部或边上时,连接 , 与 的数量关系是 , 与 的位置关系是 ;
(2)当点 在菱形 外部时,(1)中的结论是否还成立?若成立,请予以证明;若不成立,请说明理由(选择图2,图3中的一种情况予以证明或说理);
(3)如图4,当点 在线段 的延长线上时,连接 ,若 , ,求四边形 的面积.