如图,已知等腰三角形 , .若以点 为圆心, 长为半径画弧,交腰 于点 ,则下列结论一定正确的是
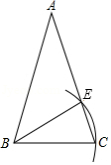
A. B. C. D.
已知 中, , , ,任作一条直线将 分成两个三角形,若其中有一个三角形是等腰三角形,则这样的直线最多有
A.3条B.5条C.7条D.8条
如图,在 中, ,点 和 分别在 和 上,且 .连接 ,过点 的直线 与 平行,若 ,则 的度数为

| A. |
|
B. |
|
C. |
|
D. |
|
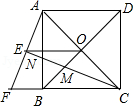
如图,正方形 的对角线 , 相交于点 ,延长 至点 ,使 ,连接 , 的平分线分别交 , , 于点 , , ,连接 .
(1)已知 ,求正方形 的边长;
(2)猜想线段 与 的数量关系并加以证明.
已知 , , 为直线 上一点, 为直线 上一点, ,设 , .
(1)如图,若点 在线段 上,点 在线段 上.
①如果 , ,那么 , .
②求 , 之间的关系式.
(2)是否存在不同于以上②中的 , 之间的关系式?若存在,求出这个关系式(求出一个即可);若不存在,说明理由.

如图, 和 都是等腰直角三角形, ,反比例函数 在第一象限的图象经过点 ,则 与 的面积之差 为

A.36B.12C.6D.3
如图, 的外角 的平分线与它的外接圆相交于点 ,连接 , ,过点 作 ,交 于点 .
求证:(1) ;
(2) 为 的切线.

如图, 是半圆 的直径, 是半圆上的一点, 平分 交半圆于点 ,过点 作 与 的延长线交于点 .
(1)求证: 是半圆的切线;
(2)若 , ,求半圆的直径.

如图,在 中, ,过 延长线上的点 作 ,交 的延长线于点 ,以 为圆心, 长为半径的圆过点 .
(1)求证:直线 与 相切;
(2)若 , 的半径为12,则 .

如图,在 中, , ,分别以点 , 为圆心, 的长为半径作弧,两弧交于点 ,连接 , ,则四边形 的面积为

A. B.9C.6D.
函数 的图象与 轴、 轴分别交于 、 两点,点 在 轴上.若 为等腰三角形,则满足条件的点 共有 个.