已知:如图, ,射线 上一点 .
求作:等腰 ,使线段 为等腰 的底边,点 在 内部,且点 到 两边的距离相等.
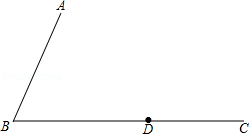
已知 中, , , ,任作一条直线将 分成两个三角形,若其中有一个三角形是等腰三角形,则这样的直线最多有
A.3条B.5条C.7条D.8条
如图,若 内一点 满足 ,则称点 为 的布罗卡尔点,三角形的布罗卡尔点是法国数学家和数学教育家克雷尔首次发现,后来被数学爱好者法国军官布罗卡尔重新发现,并用他的名字命名,布罗卡尔点的再次发现,引发了研究“三角形几何”的热潮.已知 中, , , 为 的布罗卡尔点,若 ,则 .

某城市几条道路的位置关系如图所示,已知 , 与 的夹角为 ,若 与 的长度相等,则 的度数为
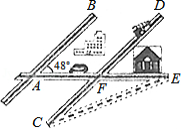
A. B. C. D.
如图,在 中, , 和 关于直线 对称,连接 ,与 相交于点 ,过点 作 ,垂足为 , 相交于点 ,若 , ,则 的值为

A. B. C. D.
如图, 是 的直径, 切 于点 ,连接 并延长交 于点 ,连接 , , ,则 的长度是
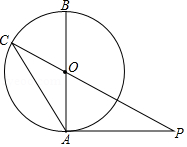
A. B. C.5D.
如图, 是半圆 的直径, 是半圆上的一点, 平分 交半圆于点 ,过点 作 与 的延长线交于点 .
(1)求证: 是半圆的切线;
(2)若 , ,求半圆的直径.

如图,在 中, ,过 延长线上的点 作 ,交 的延长线于点 ,以 为圆心, 长为半径的圆过点 .
(1)求证:直线 与 相切;
(2)若 , 的半径为12,则 .

如图,在 中, , ,分别以点 , 为圆心, 的长为半径作弧,两弧交于点 ,连接 , ,则四边形 的面积为

A. B.9C.6D.
函数 的图象与 轴、 轴分别交于 、 两点,点 在 轴上.若 为等腰三角形,则满足条件的点 共有 个.
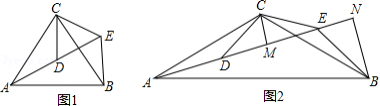
如图, 和 均为等腰三角形,点 , , 在同一直线上,连接 .
(1)如图1,若
①求证: ;
②求 的度数.
(2)如图2,若 , 为 中 边上的高, 为 中 边上的高,试证明: .