初中数学等腰三角形的性质解答题

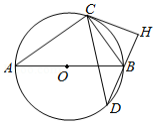
如图，为的直径，为上的一点，，，的延长线交于点，连接．

（1）求证：是的切线；

（2）若为的中点，求的值．

我们知道，各个角都相等，各条边都相等的多边形叫做正多边形．对一个各条边都相等的凸多边形（边数大于，可以由若干条对角线相等判定它是正多边形．例如，各条边都相等的凸四边形，若两条对角线相等，则这个四边形是正方形．

（1）已知凸五边形的各条边都相等．

①如图1，若，求证：五边形是正五边形；

②如图2，若，请判断五边形是不是正五边形，并说明理由：

（2）判断下列命题的真假．（在括号内填写“真”或“假”

如图3，已知凸六边形的各条边都相等．

①若，则六边形是正六边形；　　

②若，则六边形是正六边形．　　

如图，在等腰中，，以为直径作交于点，过点作，垂足为．

（1）求证：是的切线．

（2）若，，求的长．

定义：有两个相邻内角互余的四边形称为邻余四边形，这两个角的夹边称为邻余线．

（1）如图1，在中，，是的角平分线，，分别是，上的点．

求证：四边形是邻余四边形．

（2）如图2，在的方格纸中，，在格点上，请画出一个符合条件的邻余四边形，使是邻余线，，在格点上．

（3）如图3，在（1）的条件下，取中点，连结并延长交于点，延长交于点．若为的中点，，，求邻余线的长．

如图，在中，．

（1）已知线段的垂直平分线与边交于点，连接，求证：．

（2）以点为圆心，线段的长为半径画弧，与边交于点，连接．若，求的度数．

如图，在中，，于点．

（1）若，求的度数；

（2）若点在边上，交的延长线于点．求证：．

如图，是以为底的等腰三角形，是边上的高，点、分别是、的中点．

（1）求证：四边形是菱形；

（2）如果四边形的周长为12，两条对角线的和等于7，求四边形的面积．

如图，在中，，点在上，以为半径作，与相交于点，与相切于点，过点作，垂足为．

（1）求证：是的切线；

（2）若，，求的半径．

如图，在中，，是的中点，与相切于点，交于点

（1）求证：是的切线；

（2）若，点是上一个动点（不与，两点重合），求的度数．

已知，分别与相切于点，，，为上一点．

（Ⅰ）如图①，求的大小；

（Ⅱ）如图②，为的直径，与相交于点．若，求的大小．

已知是的直径，是的切线，，交于点，是上一点，延长交于点．

（1）如图①，求和的大小；

（2）如图②，当时，求的大小．

如图，内接于，且为的直径，，与交于点，与过点的的切线交于点．

（1）若，，求的长．

（2）试判断与的数量关系，并说明理由．

请阅读下列材料，并完成相应的任务：

阿基米德折弦定理

阿基米德 $(\mathit{archimedes}$ ，公元前 $287-$ 公元前212年，古希腊）是有史以来最伟大的数学家之一，他与牛顿、高斯并称为三大数学王子．

阿拉伯 $\mathit{Al}-\mathit{Binmi}(973-1050$ 年）的译文中保存了阿基米德折弦定理的内容，苏联在1964年根据 $\mathit{Al}-\mathit{Binmi}$ 译本出版了俄文版《阿基米德全集》，第一题就是阿基米德折弦定理．

阿基米德折弦定理：如图1， $\mathit{AB}$ 和 $\mathit{BC}$ 是 $\odot O$ 的两条弦（即折线 $\mathit{ABC}$ 是圆的一条折弦）， $\mathit{BC}>\mathit{AB}$ ， $M$ 是 $\stackrel{̂}{\mathit{ABC}}$ 的中点，则从 $M$ 向 $\mathit{BC}$ 所作垂线的垂足 $D$ 是折弦 $\mathit{ABC}$ 的中点，即 $\mathit{CD}=\mathit{AB}+\mathit{BD}$ ．下面是运用"截长法"证明 $\mathit{CD}=\mathit{AB}+\mathit{BD}$ 的部分证明过程．证明：如图2，在 $\mathit{CB}$ 上截取 $\mathit{CG}=\mathit{AB}$ ，连接 $\mathit{MA}$ ， $\mathit{MB}$ ， $\mathit{MC}$ 和 $\mathit{MG}$ ．

$\because M$ 是 $\stackrel{̂}{\mathit{ABC}}$ 的中点，

$\therefore \mathit{MA}=\mathit{MC}$ ．

$\dots$

任务：

（1）请按照上面的证明思路，写出该证明的剩余部分；

（2）填空：如图3，已知等边 $\mathit{\Delta ABC}$ 内接于 $\odot O$ ， $\mathit{AB}=2$ ， $D$ 为 $\stackrel{̂}{\mathit{AC}}$ 上一点， $\angle \mathit{ABD}=45°$ ， $\mathit{AE}\perp \mathit{BD}$ 于点 $E$ ，则 $\mathit{\Delta BDC}$ 的周长是 　 ．

如图，在中，，是边的中点，延长到点，使，延长到点，使，连接，，求证：．

在中，，点在以为直径的半圆内．请仅用无刻度的直尺分别按下列要求画图（保留画图痕迹）．

（1）在图1中作弦，使；

（2）在图2中以为边作一个的圆周角．