如图,在菱形 中, 是对角线 上一动点,过点 作 于点 . 于点 .若菱形 的周长为20,面积为24,则 的值为

| A. |
4 |
B. |
|
C. |
6 |
D. |
|
在 中, , 交 的延长线于点 .

特例感知:
(1)将一等腰直角三角尺按图1所示的位置摆放,该三角尺的直角顶点为 ,一条直角边与 重合,另一条直角边恰好经过点 .通过观察、测量 与 的长度,得到 .请给予证明.
猜想论证:
(2)当三角尺沿 方向移动到图2所示的位置时,一条直角边仍与 边重合,另一条直角边交 于点 ,过点 作 垂足为 .此时请你通过观察、测量 、 与 的长度,猜想并写出 、 与 之间存在的数量关系,并证明你的猜想.
联系拓展:
(3)当三角尺在图2的基础上沿 方向继续移动到图3所示的位置(点 在线段 上,且点 与点 不重合)时,请你判断(2)中的猜想是否仍然成立?(不用证明)
如图,四边形 是矩形,延长 到点 ,使 ,连接 ,点 是 的中点,连接 , ,得到△ ;点 是 的中点,连接 , ,得到△ ;点 是 的中点,连接 , ,得到△ ; ;按照此规律继续进行下去,若矩形 的面积等于2,则△ 的面积为 .(用含正整数 的式子表示)
中, , , ,过点 的直线把 分割成两个三角形,使其中只有一个是等腰三角形,则这个等腰三角形的面积是 .
图①、图②、图③均是 的正方形网格,每个小正方形的边长为1,每个小正方形的顶点称为格点,线段 的端点均在格点上,只用无刻度的直尺,在给定的网格中,按下列要求以 为边画 .
要求:
(1)在图①中画一个钝角三角形,在图②中画一个直角三角形,在图③中画一个锐角三角形;
(2)三个图中所画的三角形的面积均不相等;
(3)点 在格点上.

如图,在 中, , ,点C是 的中点,以OC为半径作 .
(1)求证: 是 的切线;
(2)若 ,求 的长.

如图,在 中,按以下步骤作图:
①以点 为圆心,任意长为半径作弧,分别交 、 于点 、 .
②分别以点 、 为圆心,大于 的同样长为半径作弧,两弧交于点 .
③作射线 交 于点 .
如果 , , 的面积为18,则 的面积为 .

如图,在 中, ,以顶点 为圆心,适当长为半径画弧,分别交 , 于点 , ,再分别以点 , 为圆心,大于 的长为半径画弧,两弧交于点 ,作射线 交 于点 .若 , ,则 的面积是 .

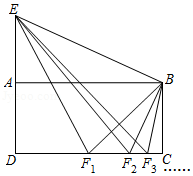
如图,平面直角坐标系中,已知点 的坐标为 .
(1)请用直尺(不带刻度)和圆规作一条直线 ,它与 轴和 轴的正半轴分别交于点 和点 ,且使 , 与 的面积相等.(作图不必写作法,但要保留作图痕迹.
(2)问:(1)中这样的直线 是否唯一?若唯一,请说明理由;若不唯一,请在图中画出所有这样的直线 ,并写出与之对应的函数表达式.
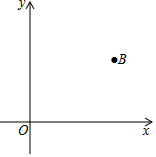
如图, 中, , , ,点 为 的中点,以 为圆心,以 为半径作半圆,交 于点 ,则图中阴影部分的面积是 .

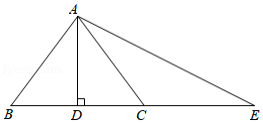
如图,在 中, ,垂足为 , ,延长 至 ,使得 ,连接 .
(1)求证: ;
(2)若 , ,求 的周长和面积.
如图1,直角三角形纸片的一条直角边长为2,剪四块这样的直角三角形纸片,把它们按图2放入一个边长为3的正方形中(纸片在结合部分不重叠无缝隙),则图2中阴影部分面积为 .

我国南宋著名数学家秦九韶在他的著作《数书九章》一书中,给出了著名的秦九韶公式,也叫三斜求积公式,即如果一个三角形的三边长分别为 , , ,则该三角形的面积为 .现已知 的三边长分别为1,2, ,则 的面积为 .
