某景区修建一栋复古建筑,其窗户设计如图所示.圆 的圆心与矩形 对角线的交点重合,且圆与矩形上下两边相切 为上切点),与左右两边相交 , 为其中两个交点),图中阴影部分为不透光区域,其余部分为透光区域.已知圆的半径为 ,根据设计要求,若 ,则此窗户的透光率(透光区域与矩形窗面的面积的比值)为 .
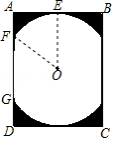
如图,已知抛物线经过两点A(﹣3,0),B(0,3),且其对称轴为直线x=﹣1.
(1)求此抛物线的解析式;
(2)若点P是抛物线上点A与点B之间的动点(不包括点A,点B),求△PAB的面积的最大值,并求出此时点P的坐标.
如图,在正方形 中, ,点 , 分别在 , 上, , , 相交于点 .若图中阴影部分的面积与正方形 的面积之比为 ,则 的周长为 .

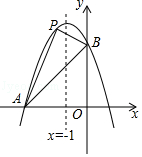
如图,点,
,
是直线
与反比例函数
图象的两个交点,
轴,垂足为点
,已知
,连接
,
,
.
(1)求直线的表达式;
(2)和
的面积分别为
,
.求
.

如图,面积为1的等腰直角△ , ,且 为斜边在△ ,外作等腰直角△ ,以 为斜边在△ ,外作等腰直角△ ,以 为斜边在△ ,外作等腰直角△ , 连接 , , , 分别与 , , , 交于点 , , , 按此规律继续下去,记△ 的面积为 ,△ 的面积为 ,△ 的面积为 , △ 的面积为 ,则 (用含正整数 的式子表示).

双曲线为常数,且
与直线
,交于
,
,
两点.
(1)求与
的值;
(2)如图,直线交
轴于点
,交
轴于点
,若点
为
的中点,求
的面积.
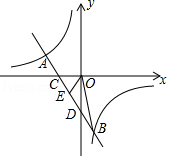
如图, 是面积为 的 内任意一点, 的面积为 , 的面积为 ,则

A. B.
C. D. 的大小与 点位置有关
如图,在正方形 的对角线 上取一点 .使得 ,连接 并延长 到 ,使 , 与 相交于点 ,若 ,有下列结论:① ;② ;③ ;④ .则其中正确的结论有

| A. |
①②③ |
B. |
①②③④ |
C. |
①②④ |
D. |
①③④ |
如图, 的面积为16,点 是 边上一点,且 ,点 是 上一点,点 在 内部,且四边形 是平行四边形,则图中阴影部分的面积是

A.3B.4C.5D.6
如图, 中, , , ,点 为 的中点,以 为圆心,以 为半径作半圆,交 于点 ,则图中阴影部分的面积是 .

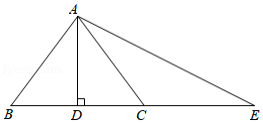
如图,在 中, ,垂足为 , ,延长 至 ,使得 ,连接 .
(1)求证: ;
(2)若 , ,求 的周长和面积.
如图1,直角三角形纸片的一条直角边长为2,剪四块这样的直角三角形纸片,把它们按图2放入一个边长为3的正方形中(纸片在结合部分不重叠无缝隙),则图2中阴影部分面积为 .

我国南宋著名数学家秦九韶在他的著作《数书九章》一书中,给出了著名的秦九韶公式,也叫三斜求积公式,即如果一个三角形的三边长分别为 , , ,则该三角形的面积为 .现已知 的三边长分别为1,2, ,则 的面积为 .
