如图,在 中, , 是 的中点,过点 作 的平行线交 于点 ,作 的垂线交 于点 ,若 ,且 的面积为1,则 的长为

A. B.5C. D.10
一次函数 的图象经过点 ,且与 轴、 轴分别交于点 、 ,则 的面积是
A. B. C.4D.8
如图, 轴于点 ,点 在 轴的正半轴上, , , ,点 为 与反比例函数 的图象的交点 . 若直线 将 的面积分成 的两部分, 则 的值为 .

如图, 的面积是12,点 、 、 、 分别是 、 、 、 的中点,则 的面积是
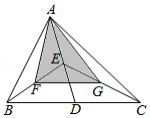
A.4.5B.5C.5.5D.6
三角形的下列线段中能将三角形的面积分成相等两部分的是
A.中线B.角平分线C.高D.中位线
如图, 的半径 垂直于弦 ,垂足为点 ,连接 并延长交 于点 ,连接 , .若 , ,则 的面积为

A.12B.15C.16D.18
如图,点 是矩形 的边 上的一动点,矩形的两条边 、 的长分别是6和8,则点 到矩形的两条对角线 和 的距离之和是

A.4.8B.5C.6D.7.2
如图,三角形纸片 ,点 是 边上一点,连接 ,把 沿着 翻折,得到 , 与 交于点 ,连接 交 于点 .若 , , , 的面积为2,则点 到 的距离为

A. B. C. D.
如图, 中, , , ,点 为 的中点,以 为圆心,以 为半径作半圆,交 于点 ,则图中阴影部分的面积是 .

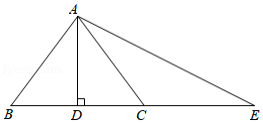
如图,在 中, ,垂足为 , ,延长 至 ,使得 ,连接 .
(1)求证: ;
(2)若 , ,求 的周长和面积.
如图1,直角三角形纸片的一条直角边长为2,剪四块这样的直角三角形纸片,把它们按图2放入一个边长为3的正方形中(纸片在结合部分不重叠无缝隙),则图2中阴影部分面积为 .

我国南宋著名数学家秦九韶在他的著作《数书九章》一书中,给出了著名的秦九韶公式,也叫三斜求积公式,即如果一个三角形的三边长分别为 , , ,则该三角形的面积为 .现已知 的三边长分别为1,2, ,则 的面积为 .
