如图,在 中, , .分别以点 , 为圆心,大于 的长为半径画弧,两弧交于 , 两点,直线 交 于点 ,连接 .以点 为圆心, 为半径画弧,交 延长线于点 ,连接 .若 ,则 的周长为 .

如图,在 中, 为 的中点,连接 并延长交 的延长线于点 ,连接 , ,若 ,求证:四边形 是矩形.

如图所示,小明家与小华家住在同一栋楼的同一单元,他俩想测算所住楼对面商业大厦的高 .他俩在小明家的窗台 处,测得商业大厦顶部 的仰角 的度数,由于楼下植物的遮挡,不能在 处测得商业大厦底部 的俯角的度数.于是,他俩上楼来到小华家,在窗台 处测得大厦底部 的俯角 的度数,竟然发现 与 恰好相等.已知 , , 三点共线, , , , ,试求商业大厦的高 .

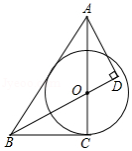
如图,在 中, 为 上一点,以点 为圆心, 为半径做圆,与 相切于点 ,过点 作 交 的延长线于点 ,且 .
(1)求证: 为 的切线;
(2)若 , ,求 的长.
如图,正方形 中, 是对角线 上一点,且 ,则 的度数为

A. B. C. D.
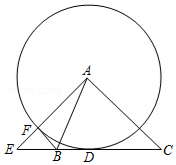
如图,在 中, , 与 相切于点 ,过点 作 的垂线交 的延长线于点 ,交 于点 ,连结 .
(1)求证: 是 的切线.
(2)若 , ,求 的长.
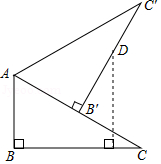
如图,在 中, , ,将 绕点 旋转得到 △ ,使点 的对应点 落在 上,在 上取点 ,使 ,那么点 到 的距离等于
A. B. C. D.
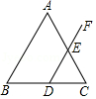
如图,在 中, , ,点 是 边上任意一点,过点 作 交 于点 ,则 的度数是
A. B. C. D.
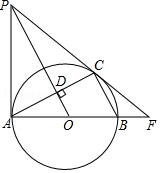
如图, 、 分别是 的直径和弦, 于点 .过点 作 的切线与 的延长线交于点 , 、 的延长线交于点 .
(1)求证: 是 的切线;
(2)若 , ,求线段 的长.
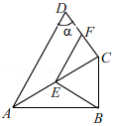
如图,四边形 中, 平分 , , 、 分别为 、 的中点, ,则 的度数为 (用含 的式子表示).
对给定的一张矩形纸片 进行如下操作:先沿 折叠,使点 落在 边上(如图① ,再沿 折叠,这时发现点 恰好与点 重合(如图②
(1)根据以上操作和发现,求 的值;
(2)将该矩形纸片展开.
①如图③,折叠该矩形纸片,使点 与点 重合,折痕与 相交于点 ,再将该矩形纸片展开.求证: ;
②不借助工具,利用图④探索一种新的折叠方法,找出与图③中位置相同的 点,要求只有一条折痕,且点 在折痕上,请简要说明折叠方法.(不需说明理由)

如图,在 中, ,点 在 上.
(1)求作: ,使点 在 上,且 ;(要求:尺规作图,保留作图痕迹,不写作法)
(2)在(1)的条件下,若 .求证: .
