问题呈现
如图1,在边长为1的正方形网格中,连接格点 , 和 , , 和 相交于点 ,求 的值.
方法归纳
求一个锐角的三角函数值,我们往往需要找出(或构造出)一个直角三角形.观察发现问题中 不在直角三角形中,我们常常利用网格画平行线等方法解决此类问题,比如连接格点 , ,可得 ,则 ,连接 ,那么 就变换到 中.
问题解决
(1)直接写出图1中 的值为 2 ;
(2)如图2,在边长为1的正方形网格中, 与 相交于点 ,求 的值;
思维拓展
(3)如图3, , ,点 在 上,且 ,延长 到 ,使 ,连接 交 的延长线于点 ,用上述方法构造网格求 的度数.

如图,一次函数 与反比例函数 的图象交于 , 两点,点 在以 为圆心,1为半径的 上, 是 的中点,已知 长的最大值为 ,则 的值为

A. B. C. D.
如图,在 中, 的平分线 交 边于点 , 于点 .已知 , .
(1)求证: ;
(2)若 ,求 的面积.

如图,矩形 中, , 相交于点 ,过点 作 交 于点 ,交 于点 ,过点 作 交 于点 ,交 于点 ,连接 , .则下列结论:
① ;
② ;
③ ;
④当 时,四边形 是菱形.
其中,正确结论的个数是

| A. |
1个 |
B. |
2个 |
C. |
3个 |
D. |
4个 |
如图,在 的正方形网格中有两个格点 、 ,连接 ,在网格中再找一个格点 ,使得 是等腰直角三角形,满足条件的格点 的个数是

| A. |
2 |
B. |
3 |
C. |
4 |
D. |
5 |
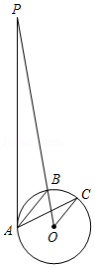
如图, 是 的切线,点 为切点, 交 于点 , ,点 在 上, .则 等于
| A. |
|
B. |
|
C. |
|
D. |
|
在① ,② ,③ 这三个条件中选择其中一个,补充在下面的问题中,并完成问题的解答.
问题:如图,在 中, ,点 在 边上(不与点 ,点 重合),点 在 边上(不与点 ,点 重合),连接 , , 与 相交于点 .若 ① ② 或 ③ ,求证: .
注:如果选择多个条件分别作答,按第一个解答计分.

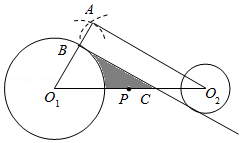
已知 的半径为 , 的半径为 .以 为圆心,以 的长为半径画弧,再以线段 的中点 为圆心,以 的长为半径画弧,两弧交于点 ,连接 , , 交 于点 ,过点 作 的平行线 交 于点 .
(1)求证: 是 的切线;
(2)若 , , ,求阴影部分的面积.
如图, 、 、 分别是 各边的中点,连接 、 、 .
(1)求证:四边形 为平行四边形;
(2)加上条件 后,能使得四边形 为菱形,请从① ;② 平分 ;③ 这三个条件中选择1个条件填空(写序号),并加以证明.

我们知道,两点之间线段最短,因此,连接两点间线段的长度叫做两点间的距离;同理,连接直线外一点与直线上各点的所有线段中,垂线段最短,因此,直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.类似地,连接曲线外一点与曲线上各点的所有线段中,最短线段的长度,叫做点到曲线的距离.依此定义,如图,在平面直角坐标系中,点 到以原点为圆心,以1为半径的圆的距离为 .
