小明将两个直角三角形纸片如图(1)那样拼放在同一平面上,抽象出如图(2)的平面图形, 与 恰好为对顶角, ,连接 , ,点 是线段 上一点.
探究发现:
(1)当点 为线段 的中点时,连接 (如图(2) ,小明经过探究,得到结论: .你认为此结论是否成立? .(填"是"或"否"
拓展延伸:
(2)将(1)中的条件与结论互换,即: ,则点 为线段 的中点.请判断此结论是否成立.若成立,请写出证明过程;若不成立,请说明理由.
问题解决:
(3)若 , ,求 的长.

如图,把含 的直角三角板 放置在正方形 中, ,直角顶点 在正方形 的对角线 上,点 , 分别在 和 边上, 与 交于点 ,且点 为 的中点,则 的度数为

| A. |
|
B. |
|
C. |
|
D. |
|
已知:如图,矩形 的对角线 , 相交于点 , , .
(1)求矩形对角线的长;
(2)过 作 于点 ,连结 .记 ,求 的值.
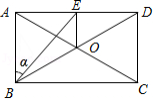
如图,在 中, 是 边上的中线,以 为直径的 交 于点 ,过 作 于点 ,交 的延长线于点 ,过点 作 于 .
(1)求证: ;
(2)求证:直线 是 的切线.

如图,正三角形 的边长为3,将 绕它的外心 逆时针旋转 得到△ ,则它们重叠部分的面积是

A. B. C. D.
如图1,直角三角形纸片的一条直角边长为2,剪四块这样的直角三角形纸片,把它们按图2放入一个边长为3的正方形中(纸片在结合部分不重叠无缝隙),则图2中阴影部分面积为 .

把一张宽为 的长方形纸片 折叠成如图所示的阴影图案,顶点 , 互相重合,中间空白部分是以 为直角顶点,腰长为 的等腰直角三角形,则纸片的长 (单位: 为

A. B. C. D.
如图, 为等腰直角三角形,延长 至点 使 , 是矩形,其对角线 , 交于点 ,连接 交 于点 .
(1)求证: ;
(2)求 的值.

如图, 的顶点 , ,点 在 轴的正半轴上,延长 交 轴于点 .将 绕点 顺时针旋转得到△ ,当点 的对应点 落在 上时, 的延长线恰好经过点 ,则点 的坐标为

| A. |
, |
B. |
, |
C. |
, |
D. |
, |
定理:三角形的一个外角等于与它不相邻的两个内角的和.
已知:如图, 是 的外角.求证: .
| 证法1:如图, (三角形内角和定理), 又 (平角定义), (等量代换). (等式性质). |
| 证法2:如图, , , 且 (量角器测量所得) 又 (计算所得) (等量代换). |
下列说法正确的是

| A. |
证法1还需证明其他形状的三角形,该定理的证明才完整 |
| B. |
证法1用严谨的推理证明了该定理 |
| C. |
证法2用特殊到一般法证明了该定理 |
| D. |
证法2只要测量够一百个三角形进行验证,就能证明该定理 |
如图,△ 为等腰直角三角形, ,以斜边 为直角边作等腰直角三角形 ,再以 为直角边作等腰直角三角形 , ,按此规律作下去,则 的长度为
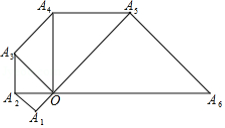
A. B. C. D.
已知 , 是等腰三角形的两边长,且 , 满足 ,则此等腰三角形的周长为
| A. |
8 |
B. |
6或8 |
C. |
7 |
D. |
7或8 |
如图,菱形 的顶点 , , 在 上,过点 作 的切线交 的延长线于点 .若 的半径为1,则 的长为
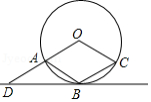
A.1B.2C. D.