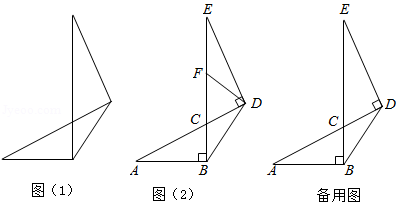
小明将两个直角三角形纸片如图（1）那样拼放在同一平面上，抽象出如图（2）的平面图形， 与 恰好为对顶角， ，连接 ， ，点 是线段 上一点．
探究发现：
（1）当点 为线段 的中点时，连接 （如图（2） ，小明经过探究，得到结论： ．你认为此结论是否成立？ ．（填"是"或"否"
拓展延伸：
（2）将（1）中的条件与结论互换，即： ，则点 为线段 的中点．请判断此结论是否成立．若成立，请写出证明过程；若不成立，请说明理由．
问题解决：
（3）若 ， ，求 的长．
近年来，有私家车的业主越来越多，某小区为解决“停车难”问题，拟建造一个地下停车库．如图是该地下停车库坡道入口的设计示意图，其中水平线AB=10m，BD⊥AB，∠BAD=20°，点C在BD上，BC=1m．根据规定，地下停车库坡道入口上方要张贴限高标志，以提醒驾驶员所驾车辆能否安全驶入．李建认为CD的长度就是限制的高度，而孙杰认为应该以CE的长度作为限制的高度．李建和孙杰谁说的对？请你判断并计算出限制高度．（结果精确到0.1m，参考数据：sin20°≈0.34，cos20°≈0.94，tan20°≈0.36）
某中学为了了解本校八年级女生“一分钟跳绳”项目基础情况，从八年级随机抽取部分女生进行该项目测试，并将测试所得的数据，绘制成如图所示的部分频数分布直方图（从左到右依次分为第一小组，第二小组…第六小组，每小组含最小值，不含最大值）和扇形统计图．根据统计图提供的信息解答下列问题：
（1）补全频数分布直方图．
（2）计算在扇形统计图中第一小组对应的扇形的圆心角度数．
（3）这次测试成绩的中位数落在第 小组．
（4）若测试八年级女生“一分钟跳绳”次数不低于130次的成绩为优秀，本校八年级女生共有400人，请估算该校八年级女生“一分钟跳绳”成绩为优秀的人数．
“大湖名城•创新高地•中国合肥”，为了让学生亲身感受合肥城市的变化，蜀山中学九（1）班组织学生进行“环巢湖一日研学游”活动，某旅行社推出了如下收费标准：（1）如果人数不超过30人，人均旅游费用为100元；（2）如果超过30人，则每超过1人，人均旅游费用降低2元，但人均旅游费用不能低于80元．该班实际共支付给旅行社3150元，问：共有多少名同学参加了研学游活动？
如图，在由边长为1的单位正方形组成的网格中，按要求画出坐标系及△A1B1C1及△A2B2C2；
（1）若点A、C的坐标分别为（﹣3，0）、（﹣2，3），请画出平面直角坐标系并指出点B的坐标；
（2）画出△ABC关于y轴对称再向上平移1个单位后的图形△A1B1C1；
（3）以图中的点D为位似中心，将△A1B1C1作位似变换且把边长放大到原来的两倍，得到△A2B2C2．
、﹣
、﹣
这六个数按此规律重复出现．问：
粤公网安备 44130202000953号