如图,菱形 的对角线 、 相交于点 , 、 分别为边 、 的中点,连接 .若 , ,则菱形的周长为 .

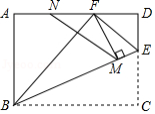
在矩形纸片 中, , , 是边 上的点,将纸片沿 折叠,使点 落在点 处,连接 ,当 为直角三角形时, 的长为 .
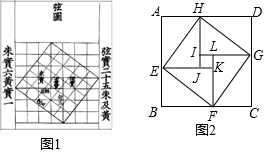
我国三国时期数学家赵爽为了证明勾股定理,创造了一幅“弦图”,后人称其为“赵爽弦图”,如图1所示.在图2中,若正方形 的边长为14,正方形 的边长为2,且 ,则正方形 的边长为 .
如图,在平面直角坐标系中,正方形 的顶点 的坐标为 ,点 在 轴正半轴上,点 在第三象限的双曲线 上,过点 作 轴交双曲线于点 ,连接 ,则 的面积为 .

如图, 是等边三角形,点 为 边上一点, ,以点 为顶点作正方形 ,且 ,连接 , .若将正方形 绕点 旋转一周,当 取最小值时, 的长为 .
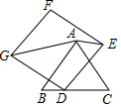
如图, 是等边三角形, ,分别以 , , 为圆心,以2为半径作弧,则图中阴影部分的面积是 .

如图1,在矩形纸片 中, , ,点 是 中点,将这张纸片依次折叠两次;第一次折叠纸片使点 与点 重合,如图2,折痕为 ,连接 、 ;第二次折叠纸片使点 与点 重合,如图3,点 落到 处,折痕为 ,连接 ,则 .

如图,矩形纸片 , , , 为边 上一点.将 沿 所在的直线折叠,点 恰好落在 边上的点 处,过点 作 ,垂足为点 ,取 的中点 ,连接 ,则 .