如图, 为反比例函数 (其中 图象上的一点,在 轴正半轴上有一点 , .连接 , ,且 .
(1)求 的值;
(2)过点 作 ,交反比例函数 (其中 的图象于点 ,连接 交 于点 ,求 的值.

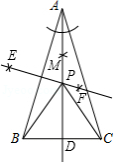
如图, 中, ,小聪同学利用直尺和圆规完成了如下操作:
①作 的平分线 交 于点 ;
②作边 的垂直平分线 , 与 相交于点 ;
③连接 , .
请你观察图形解答下列问题:
(1)线段 , , 之间的数量关系是 ;
(2)若 ,求 的度数.
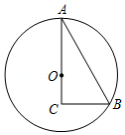
如图,在 中, , , ,以边 上一点 为圆心, 为半径的 经过点 .
(1)求 的半径;
(2)点 为劣弧 中点,作 ,垂足为 ,求 的长;
(3)在(2)的条件下,连接 ,求 的值.
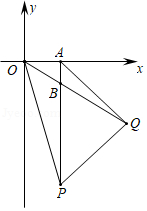
如图, 是平面直角坐标系中第四象限内一点,过点 作 轴于点 ,以 为斜边在右侧作等腰 ,已知直角顶点 的纵坐标为 ,连接 交 于 , .
(1)求点 的坐标;
(2)连接 ,求 的面积与 的面积之比.
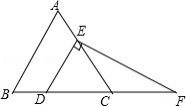
如图,在 中, , , 的外角 的平分线 交 的延长线于点 .
(1)求 的度数;
(2)过点 作 ,交 的延长线于点 ,求 的度数.

问题:如图①,在 中, , 为 边上一点(不与点 , 重合),将线段 绕点 逆时针旋转 得到 ,连接 ,则线段 , , 之间满足的等量关系式为 ;
探索:如图②,在 与 中, , ,将 绕点 旋转,使点 落在 边上,试探索线段 , , 之间满足的等量关系,并证明你的结论;
应用:如图③,在四边形 中, .若 , ,求 的长.

如图,在 中,半径 ,过点 的中点 作 交 于 、 两点,且 ,以 为圆心, 为半径作 ,交 于 点.
(1)求 的半径 的长;
(2)计算阴影部分的面积.

在等边 中,点 , 分别在边 、 上,若 ,过点 作 ,过点 作 ,交 的延长线于点 ,求 的长.
如图,分别是可活动的菱形和平行四边形学具,已知平行四边形较短的边与菱形的边长相等.
(1)在一次数学活动中,某小组学生将菱形的一边与平行四边形较短边重合,摆拼成如图1所示的图形, 经过点 ,连接 交 于点 ,观察发现:点 是 的中点.
下面是两位学生有代表性的证明思路:
思路1:不需作辅助线,直接证三角形全等;
思路2:不证三角形全等,连接 交 于点 .
请参考上面的思路,证明点 是 的中点(只需用一种方法证明);
(2)如图2,在(1)的前提下,当 时,延长 、 交于点 ,求 的值;
(3)在(2)的条件下,若 为大于 的常数),直接用含 的代数式表示 的值.

阅读:能够成为直角三角形三条边长的三个正整数 , , ,称为勾股数.世界上第一次给出勾股数通解公式的是我国古代数学著作《九章算术》,其勾股数组公式为: 其中 , , 是互质的奇数.
应用:当 时,求有一边长为5的直角三角形的另外两条边长.
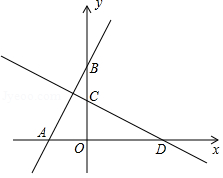
如图,在平面直角坐标系 中,过点 的直线交 轴正半轴于点 ,将直线 绕着点 顺时针旋转 后,分别与 轴、 轴交于点 、 .
(1)若 ,求直线 的函数关系式;
(2)连接 ,若 的面积是5,求点 的运动路径长.
阅读理解:
如图①,图形 外一点 与图形 上各点连接的所有线段中,若线段 最短,则线段 的长度称为点 到图形 的距离.

例如:图②中,线段 的长度是点 到线段 的距离;线段 的长度是点 到线段 的距离.
解决问题:
如图③,平面直角坐标系 中,点 、 的坐标分别为 , ,点 从原点 出发,以每秒1个单位长度的速度向 轴正方向运动了 秒.
(1)当 时,求点 到线段 的距离;
(2) 为何值时,点 到线段 的距离为5?
(3) 满足什么条件时,点 到线段 的距离不超过6?(直接写出此小题的结果)
我们规定:三角形任意两边的“极化值”等于第三边上的中线和这边一半的平方差.如图1,在 中, 是 边上的中线, 与 的“极化值”就等于 的值,可记为 △ .
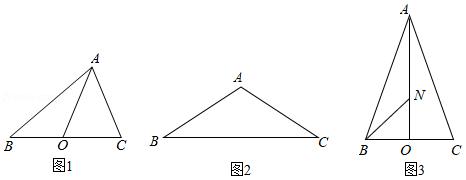
(1)在图1中,若 , , , 是 边上的中线,则 △ , △ ;
(2)如图2,在 中, , ,求 △ 、 △ 的值;
(3)如图3,在 中, , 是 边上的中线,点 在 上,且 .已知 △ , △ ,求 的面积.
已知:如图,在 中, ,点 是 的中点,且 ,点 是 的中点,过点 作 交 的延长线于点 .
(1)求证: ;
(2)若 , ,求 的长.
