阅读理解:
如图①,图形 外一点 与图形 上各点连接的所有线段中,若线段 最短,则线段 的长度称为点 到图形 的距离.
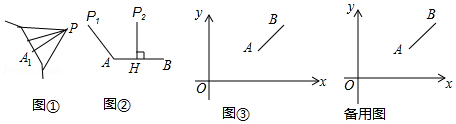
例如:图②中,线段 的长度是点 到线段 的距离;线段 的长度是点 到线段 的距离.
解决问题:
如图③,平面直角坐标系 中,点 、 的坐标分别为 , ,点 从原点 出发,以每秒1个单位长度的速度向 轴正方向运动了 秒.
(1)当 时,求点 到线段 的距离;
(2) 为何值时,点 到线段 的距离为5?
(3) 满足什么条件时,点 到线段 的距离不超过6?(直接写出此小题的结果)
推荐套卷
 ,0,﹣|﹣2.5|,﹣(﹣3),1.5,
,0,﹣|﹣2.5|,﹣(﹣3),1.5, .
.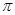 ,2.008,
,2.008, ,
, ,-
,- ,0,-(-2.28),-1.1010010001….
,0,-(-2.28),-1.1010010001….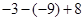



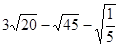
 +
+ +3
+3 -
-
 +
+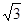 )(
)(
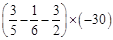
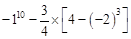
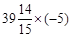 (简便运算)
(简便运算) 粤公网安备 44130202000953号
粤公网安备 44130202000953号