如图,将正 边形绕点 顺时针旋转 后,发现旋转前后两图形有另一交点 ,连接 ,我们称 为"叠弦";再将"叠弦" 所在的直线绕点 逆时针旋转 后,交旋转前的图形于点 ,连接 ,我们称 为"叠弦角", 为"叠弦三角形".
[探究证明]
(1)请在图1和图2中选择其中一个证明:"叠弦三角形" 是等边三角形;
(2)如图2,求证: .
[归纳猜想]
(3)图1、图2中的"叠弦角"的度数分别为 , ;
(4)图 中,"叠弦三角形" 等边三角形(填"是"或"不是"
(5)图 中,"叠弦角"的度数为 (用含 的式子表示)

如图是一张长方形纸片 ,已知 , , 为 上一点, ,现要剪下一张等腰三角形纸片 ,使点 落在长方形 的某一条边上,则等腰三角形 的底边长是 .

如图,点 , , , 在直线 上 , 之间不能直接测量),点 , 在 异侧,测得 , , .
(1)求证: ;
(2)指出图中所有平行的线段,并说明理由.

如图,已知 ,一条光线从点 出发后射向 边.若光线与 边垂直,则光线沿原路返回到点 ,此时 .
当 时,光线射到 边上的点 后,经 反射到线段 上的点 ,易知 .若 ,光线又会沿 原路返回到点 ,此时 .
若光线从 点出发后,经若干次反射能沿原路返回到点 ,则锐角 的最小值 .

如图, , 平分 ,且 .若点 , 分别在 , 上,且 为等边三角形,则满足上述条件的 有

| A. |
1个 |
B. |
2个 |
C. |
3个 |
D. |
3个以上 |
如图,在矩形 中, , ,动点 满足 ,则点 到 、 两点距离之和 的最小值为

| A. |
|
B. |
|
C. |
|
D. |
|
如图,在矩形纸片中,
,
,点
在
上,将
沿
折叠,点
恰落在边
上的点
处;点
在
上,将
沿
折叠,点
恰落在线段
上的点
处,有下列结论:
①;②
;③
;④
.
其中正确的是 .(把所有正确结论的序号都选上)

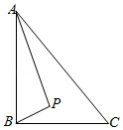
如图, 中, , , , 是 内部的一个动点,且满足 ,则线段 长的最小值为
| A. |
|
B. |
2 |
C. |
|
D. |
|
在中,
,
,
是
的中点.
为直线
上一动点,连接
.过点
作
,交直线
于点
,连接
.
(1)如图1,当是线段
的中点时,设
,
,求
的长(用含
,
的式子表示);
(2)当点在线段
的延长线上时,依题意补全图2,用等式表示线段
,
,
之间的数量关系,并证明.

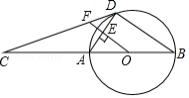
如图,为
的直径,
为
延长线上一点,
是
的切线,
为切点,
于点
,交
于点
.
(1)求证:;
(2)若,
,求
的长.
已知:如图, 为锐角三角形, , .
求作:线段 ,使得点 在直线 上,且 .
作法:①以点 为圆心, 长为半径画圆,交直线 于 , 两点;
②连接 .
线段 就是所求作的线段.
(1)使用直尺和圆规,依作法补全图形(保留作图痕迹);
(2)完成下面的证明.
证明: ,
.
,
点 在 上.
又 点 , 都在 上,
(填推理的依据).
.

如图所示的网格是正方形网格,,
,
,
是网格线交点,则的面积与
的面积的大小关系为:
(填“
”,“
”或“
”
.
