如图,在 中, , , ,将 绕点 逆时针旋转得到 △ ,使点 落在 边上,连接 ,则 的长度是

A. B. C. D.
小亮在学习中遇到这样一个问题:
如图,点 是 上一动点,线段 ,点 是线段 的中点,过点 作 ,交 的延长线于点 .当 为等腰三角形时,求线段 的长度.
小亮分析发现,此问题很难通过常规的推理计算彻底解决,于是尝试结合学习函数的经验研究此问题.请将下面的探究过程补充完整:
(1)根据点 在 上的不同位置,画出相应的图形,测量线段 , , 的长度,得到下表的几组对应值.
|
0 |
1.0 |
2.0 |
3.0 |
4.0 |
5.0 |
6.0 |
7.0 |
8.0 |
|
8.0 |
7.7 |
7.2 |
6.6 |
5.9 |
|
3.9 |
2.4 |
0 |
|
8.0 |
7.4 |
6.9 |
6.5 |
6.1 |
6.0 |
6.2 |
6.7 |
8.0 |
操作中发现:
①“当点 为 的中点时, ”.则上表中 的值是 5.0 ;
②“线段 的长度无需测量即可得到”.请简要说明理由.
(2)将线段 的长度作为自变量 , 和 的长度都是 的函数,分别记为 和 ,并在平面直角坐标系 中画出了函数 的图象,如图所示.请在同一坐标系中画出函数 的图象;
(3)继续在同一坐标系中画出所需的函数图象,并结合图象直接写出:当 为等腰三角形时,线段 长度的近似值(结果保留一位小数).


我们学习过利用尺规作图平分一个任意角,而“利用尺规作图三等分一个任意角”曾是数学史上一大难题,之后被数学家证明是不可能完成的.人们根据实际需要,发明了一种简易操作工具 三分角器.图1是它的示意图,其中 与半圆 的直径 在同一直线上,且 的长度与半圆的半径相等; 与 垂直于点 , 足够长.
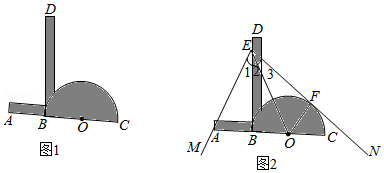
使用方法如图2所示,若要把 三等分,只需适当放置三分角器,使 经过 的顶点 ,点 落在边 上,半圆 与另一边 恰好相切,切点为 ,则 , 就把 三等分了.
为了说明这一方法的正确性,需要对其进行证明.如下给出了不完整的“已知”和“求证”,请补充完整,并写出“证明”过程.
已知:如图2,点 , , , 在同一直线上, ,垂足为点 , .
求证: .
如图,在边长为 的正方形 中,点 , 分别是边 , 的中点,连接 , ,点 , 分别是 , 的中点,连接 ,则 的长度为 .

如图,在 中, , ,分别以点 , 为圆心, 的长为半径作弧,两弧交于点 ,连接 , ,则四边形 的面积为

A. B.9C.6D.
如图,四边形 是平行四边形, ,且分别交对角线 于点 , ,连接 , .
(1)求证: ;
(2)若 ,求证:四边形 为菱形.

如图,在 轴, 轴上分别截取 , ,使 ,再分别以点 , 为圆心,以大于 长为半径画弧,两弧交于点 .若点 的坐标为 ,则 的值为 .

如图,在 中, , 是 的中点,过点 作 的平行线交 于点 ,作 的垂线交 于点 ,若 ,且 的面积为1,则 的长为

A. B.5C. D.10
在 中,弦 与直径 相交于点 , .
(Ⅰ)如图①,若 ,求 和 的大小;
(Ⅱ)如图②,若
,过点
作
的切线,与
的延长线相交于点
,求
的大小.
如图,在每个小正方形的边长为1的网格中, 的顶点 , 均落在格点上,点 在网格线上,且 .
(Ⅰ)线段 的长等于 .
(Ⅱ)以 为直径的半圆与边 相交于点 ,若 , 分别为边 , 上的动点,当 取得最小值时,请用无刻度的直尺,在如图所示的网格中,画出点 , ,并简要说明点 , 的位置是如何找到的(不要求证明) .

如图, 的顶点 在等边 的边 上,点 在 的延长线上, 为 的中点,连接 .若 , ,则 的长为 .

如图,在平行四边形 中,对角线 , 相交于点 ,分别过点 , 作 , ,垂足分别为 , . 平分 .
(1)若 ,求 的度数;
(2)求证: .

如图,在平面直角坐标系中,矩形 的对角线 的中点与坐标原点重合,点 是 轴上一点,连接 .若 平分 ,反比例函数 的图象经过 上的两点 , ,且 , 的面积为18,则 的值为

A.6B.12C.18D.24