特例感知
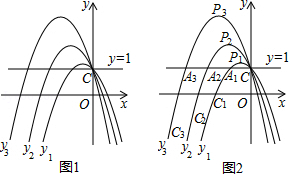
(1)如图1,对于抛物线,
,
,下列结论正确的序号是 ;
①抛物线,
,
都经过点
;
②抛物线,
的对称轴由抛物线
的对称轴依次向左平移
个单位得到;
③抛物线,
,
与直线
的交点中,相邻两点之间的距离相等.
形成概念
(2)把满足为正整数)的抛物线称为“系列平移抛物线”.
知识应用
在(2)中,如图2.
①“系列平移抛物线”的顶点依次为,
,
,
,
,用含
的代数式表示顶点
的坐标,并写出该顶点纵坐标
与横坐标
之间的关系式;
②“系列平移抛物线”存在“系列整数点(横、纵坐标均为整数的点)”:,
,
,
,
,其横坐标分别为
,
,
,
,
为正整数),判断相邻两点之间的距离是否都相等,若相等,直接写出相邻两点之间的距离;若不相等,说明理由.
③在②中,直线分别交“系列平移抛物线”于点
,
,
,
,
,连接
,
,判断
,
是否平行?并说明理由.
如图, 、 、 、 是直线 上的四点, , , .
(1)求证: ;
(2)将 沿直线 翻折得到△ .
①用直尺和圆规在图中作出△ (保留作图痕迹,不要求写作法);
②连接 ,则直线 与 的位置关系是 .

如图,在 中, ,点 在 上.
(1)求作: ,使点 在 上,且 ;(要求:尺规作图,保留作图痕迹,不写作法)
(2)在(1)的条件下,若 .求证: .

如图, D是△ ABC中 BC边上一点,∠ C=∠ DAC.
(1)尺规作图:作∠ ADB的平分线,交 AB于点 E(保留作图痕迹,不写作法);
(2)在(1)的条件下,求证: DE∥ AC.

如图,已知的半径为5,
是
的一条切线,切点为
,连接
并延长,交
于点
,过点
作
交
于点
、交
于点
,连接
,当
时,
(1)求弦的长;
(2)求证:.

(1)解方程组: .
(2)如图, 中, ,将 向下翻折,使点 与点 重合,折痕为 .求证: .

如图,点 , , , 在直线 上 , 之间不能直接测量),点 , 在 异侧,测得 , , .
(1)求证: ;
(2)指出图中所有平行的线段,并说明理由.

用反证法证明:已知直线a、b被直线c所截,∠1+∠2≠180°.求证:a与b不平行.
证明:假设_________________________,则:∠1+∠2=180°(___________________________)
这与____________________矛盾,故假设不成立.所以a与b不平行.