初中数学反比例函数综合题试题

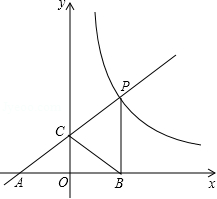
如图，在平面直角坐标系 xOy中，菱形 ABCD的对角线 AC与 BD交于点 P（﹣1，2）， AB⊥ x轴于点 E，正比例函数 y＝ mx的图象与反比例函数 y＝ $\frac{n-3}{x}$ 的图象相交于 A， P两点．

（1）求 m， n的值与点 A的坐标；

（2）求证：△ CPD∽△ AEO；

（3）求sin∠ CDB的值．

如图， A、 B是函数 y＝ $\frac{12}{x}$ 上两点， P为一动点，作 PB∥ y轴， PA∥ x轴，下列说法正确的是（　　）

①△ AOP≌△ BOP；② S _{△ AOP}＝ S _{△ BOP}；③若 OA＝ OB，则 OP平分∠ AOB；④若 S _{△ BOP}＝4，则 S _{△ ABP}＝16

A．

①③

B．

②③

C．

②④

D．

③④

设 P（ x，0）是 x轴上的一个动点，它与原点的距离为 y ₁．

（1）求 y ₁关于 x的函数解析式，并画出这个函数的图象；

（2）若反比例函数 y ₂＝ $\frac{k}{x}$ 的图象与函数 y ₁的图象相交于点 A，且点 A的纵坐标为2．

①求 k的值；

②结合图象，当 y ₁＞ y ₂时，写出 x的取值范围．

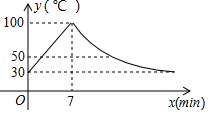
教室里的饮水机接通电源就进入自动程序，开机加热时每分钟上升10℃，加热到100℃停止加热，水温开始下降，此时水温 y（℃）与开机后用时 x（ min）成反比例关系，直至水温降至30℃，饮水机关机，饮水机关机后即刻自动开机，重复上述自动程序．若在水温为30℃时接通电源，水温 y（℃）与时间 x（ min）的关系如图所示：

（1）分别写出水温上升和下降阶段 y与 x之间的函数关系式；

（2）怡萱同学想喝高于50℃的水，请问她最多需要等待多长时间？

如图，在平面直角坐标系中，反比例函数 y＝ $\frac{k}{x}$ （ k＞0）的图象与半径为5的⊙ O交于 M、 N两点，△ MON的面积为3.5，若动点 P在 x轴上，则 PM+ PN的最小值是 　　．

已知变量 x、 y对应关系如下表已知值呈现的对应规律．

x	…	﹣4	﹣3	﹣2	﹣1	1	2	3	4	…
y	…	$\frac{1}{2}$	$\frac{2}{3}$	1	2	﹣2	﹣1	﹣     $\frac{2}{3}$	﹣     $\frac{1}{2}$	…

（1）依据表中给出的对应关系写出函数解析式，并在给出的坐标系中画出大致图象；

（2）在这个函数图象上有一点 P（ x， y）（ x＜0），过点 P分别作 x轴和 y轴的垂线，并延长与直线 y＝ x﹣2交于 A、 B两点，若△ PAB的面积等于 $\frac{25}{2}$ ，求出 P点坐标．

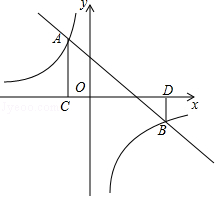
如图，直线 y＝﹣ x+2与反比例函数 y＝ $\frac{k}{x}$ （ k≠0）的图象交于 A（ a，3）， B（3， b）两点，过点 A作 AC⊥ x轴于点 C，过点 B作 BD⊥ x轴于点 D．

（1）求 a， b的值及反比例函数的解析式；

（2）若点 P在直线 y＝﹣ x+2上，且 S _{△ ACP}＝ S _{△ BDP}，请求出此时点 P的坐标；

（3）在 x轴正半轴上是否存在点 M，使得△ MAB为等腰三角形？若存在，请直接写出 M点的坐标；若不存在，说明理由．

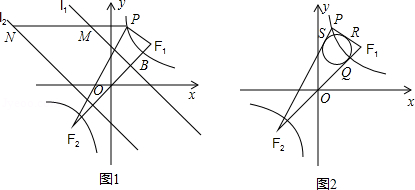
如图1所示，已知：点A（﹣2，﹣1）在双曲线 $\text{C:}y=\frac{a}{x}$上，直线l₁：y＝﹣x+2，直线l₂与l₁关于原点成中心对称，F₁（2，2），F₂（﹣2，﹣2）两点间的连线与曲线C在第一象限内的交点为B，P是曲线C上第一象限内异于B的一动点，过P作x轴平行线分别交l₁，l₂于M，N两点．

（1）求双曲线C及直线l₂的解析式；

（2）求证： $P{F}_2﹣P{F}_1＝\mathit{MN}＝4$；

（3）如图2所示，△PF₁F₂的内切圆与F₁F₂，PF₁，PF₂三边分别相切于点Q，R，S，求证：点Q与点B重合．（参考公式：在平面坐标系中，若有点A（x₁，y₁），B（x₂，y₂），则A、B两点间的距离公式为 $\mathit{AB}=\sqrt{{\left(x_1-x_2\right)}^2+{\left(y_1-y_2\right)}^2}$.

已知反比例函数 y＝ $\frac{-k^2-1}{x}$ （ k为常数）．

（1）若点 P ₁（ $\frac{1-\sqrt{3}}{2}$ ， y ₁）和点 P ₂（﹣ $\frac{1}{2}$ ， y ₂）是该反比例函数图象上的两点，试利用反比例函数的性质比较 y ₁和 y ₂的大小；

（2）设点 P（ m， n）（ m＞0）是其图象上的一点，过点 P作 PM⊥ x轴于点 M．若tan∠ POM＝2， PO＝ $\sqrt{5}$ （ O为坐标原点），求 k的值，并直接写出不等式 kx+ $\frac{k^2+1}{x}$ ＞0的解集．

如图，一次函数 y＝﹣ $\frac{\sqrt{\text{3}}}{\text{3}}$ x+1的图象与 x轴、 y轴分别交于点 A、 B，以线段 AB为边在第一象限作等边△ ABC．

（1）若点 C在反比例函数 y＝ $\frac{k}{x}$ 的图象上，求该反比例函数的解析式；

（2）点 P（2 $\sqrt{3}$ ， m）在第一象限，过点 P作 x轴的垂线，垂足为 D，当△ PAD与△ OAB相似时， P点是否在（1）中反比例函数图象上？如果在，求出 P点坐标；如果不在，请加以说明．

如图，反比例函数y＝ $\frac{k_1}{x}$与一次函数y＝k₂x+b的图象交于A（2，4），B（﹣4，m）两点．

（1）求k₁，k₂，b的值；

（2）求△AOB的面积；

（3）若M（x₁，y₁），N（x₂，y₂）是反比例函数y＝ $\frac{k_1}{x}$的图象上的两点，且x₁＜x₂，y₁＜y₂，指出点M、N各位于哪个象限．

如图， O为坐标原点，点 B在 x轴上，四边形 OACB为平行四边形，cos∠ AOB＝ $\frac{3}{5}$ ，反比例函数 y＝ $\frac{k}{x}(k>0)$ 在第一象限内的图象经过点 A，与 BC交于点 F．

（1）若 OA＝5， OB＝6，求反比例函数解析式及 C点的坐标；

（2）若点 F为 BC的中点，且△ AOF的面积为6，求 OA的长．

如图，在平面直角坐标系 xOy中，反比例函数 y＝ $\frac{m}{x}$ 的图象与一次函数 y＝ k（ x﹣2）的图象交点为 A（3，2）， B（ x， y）．

（1）求反比例函数与一次函数的解析式及 B点坐标；

（2）若 C是 y轴上的点，且满足△ ABC的面积为10，求 C点坐标．

如图，一次函数 y＝ ax+ b的图象与反比例函数 y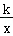＝ （ x＞0）的图象交于点 P（ m，4），与 x轴交于点 A（﹣3，0），与 y轴交于点 C， PB⊥ x轴于点 B，且 AC＝ BC．

（1）求反比例函数与一次函数的解析式；

（2）反比例函数图象上是否存在点 D，使四边形 BCPD为菱形？如果存在，求出点 D的坐标；如果不存在，说明理由．

将直线 向下平移1个单位长度，得到直线 ，若反比例函数 $y=\frac{k}{x}$ 的图象与直线 相交于点 ，且点 的纵坐标是3．

（1）求 和 的值；

（2）结合图象求不等式 $3x+m>\frac{k}{x}$ 的解集．