初中数学反比例函数综合题试题

如图，过原点的直线与反比例函数的图象交于，两点，点在第一象限．点在轴正半轴上，连结交反比例函数图象于点．为的平分线，过点作的垂线，垂足为，连结．若，的面积为8，则的值为　　．

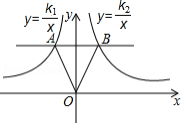
如图，在轴上方，平行于轴的直线与反比例函数和的图象分别交于、两点，连接、，若的面积为6，则　　．

模具厂计划生产面积为4，周长为的矩形模具．对于的取值范围，小亮已经能用“代数”的方法解决，现在他又尝试从“图形”的角度进行探究，过程如下：

（1）建立函数模型

设矩形相邻两边的长分别为，，由矩形的面积为4，得，即；由周长为，得，即．满足要求的应是两个函数图象在第　一　象限内交点的坐标．

（2）画出函数图象

函数的图象如图所示，而函数的图象可由直线平移得到．请在同一直角坐标系中直接画出直线．

（3）平移直线，观察函数图象

①当直线平移到与函数的图象有唯一交点时，周长的值为　　；

②在直线平移过程中，交点个数还有哪些情况？请写出交点个数及对应的周长的取值范围．

（4）得出结论

若能生产出面积为4的矩形模具，则周长的取值范围为　　．

小明在研究矩形面积与矩形的边长，之间的关系时，得到下表数据：

	0.5	1	1.5	2	3	4	6	12
	12	6	4	3	2		1	0.5

结果发现一个数据被墨水涂黑了

（1）被墨水涂黑的数据为　　．

（2）与之间的函数关系式为　　，且随的增大而　　．

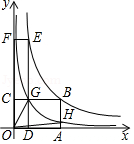
（3）如图是小明画出的关于的函数图象，点、均在该函数的图象上，其中矩形的面积记为，矩形的面积记为，请判断和的大小关系，并说明理由．

（4）在（3）的条件下，交于点，反比例函数的图象经过点交于点，连接、，则四边形的面积为　　．

如图，一次函数与反比例函数的图象交于点和．

（1）填空：一次函数的解析式为　　，反比例函数的解析式为　　；

（2）点是线段上一点，过点作轴于点，连接，若的面积为，求的取值范围．

如图，在平面直角坐标系中， $\text{Rt}\Delta \text{ABC}$ 的顶点 $A$ 、 $C$ 的坐标分别是 $(0,3)$ 、 $(3$ 、 $0)$ ． $\angle \mathit{ACB}=90°$ ， $\mathit{AC}=2\mathit{BC}$ ，则函数 $y=\frac{k}{x}(k>0,x>0)$ 的图象经过点 $B$ ，则 $k$ 的值为 $($ 　　 $)$

A．

$\frac{9}{2}$

B．

9

C．

$\frac{27}{8}$

D．

$\frac{27}{4}$

如图，两个反比例函数和在第一象限内的图象依次是C₁和C₂，设点P在C₁上，轴于点C，交C₂于点A，轴于点D，交C₂于点B，则四边形PAOB的面积为（  ）

A．2

B．3

C．4

D．5

如图，一次函数与反比例函数的图象交于、两点．

（1）求、两点的坐标和反比例函数的解析式；
（2）根据图象，直接写出当时的取值范围；
（3）求的面积．

如图，正方形ABCD的顶点B，C在x轴的正半轴上，反比例函数y=（k≠0）在第一象限的图象经过顶点A（m，2）和CD边上的点E（n，），过点E的直线l交x轴于点F，交y轴于点G（0，-2），则点F的坐标是（  ）
   

A．（，0）

B．（，0）

C．（，0）

D．（，0）

如图，一次函数（为常数，且）的图像与反比例函数的图像交于，两点．

（1）求一次函数的表达式；
（2）若将直线向下平移个单位长度后与反比例函数的图像有且只有一个公共点，求的值．

（年新疆乌鲁木齐市）如图，在直角坐标系xOy中，点A，B分别在x轴和y轴，．∠AOB的角平分线与OA的垂直平分线交于点C，与AB交于点D，反比例函数的图象过点C．当以CD为边的正方形的面积为时，k的值是（ ）

A．2      B．3      C．5      D．7

阅读理解：对于任意正实数a、b，∵(－)²≥0，∴a－2＋b≥0，∴a＋b≥2，只有当a＝b时，等号成立.
结论：在a＋b≥2（a、b均为正实数）中，若ab为定值p，则a+b≥2，只有当a＝b时，a＋b有最小值2.  根据上述内容，回答下列问题：
（1）若m＞0，只有当m＝       时，m＋有最小值         ；
若m＞0，只有当m＝       时，2m＋有最小值        .
（2）如图，已知直线L₁：y＝x＋1与x轴交于点A，过点A的另一直线L₂与双曲线y＝（x>0）相交于点B（2，m），求直线L₂的解析式.

（3）在（2）的条件下，若点C为双曲线上任意一点，作CD∥y轴交直线L₁于点D，试求当线段CD最短时，点A、B、C、D围成的四边形面积.