专题51 新定义和阅读理解型问题(预测题)
阅读下面的材料:
小明在数学课外小组活动中遇到这样一个“新定义”问题:

小明是这样解决问题的:由新定义可知a=1,b=-2,又b<0,所以1※(-2)= .
.
请你参考小明的解题思路,回答下列问题:
(1)计算:2※3= ;
(2)若5※m= ,则m= .
,则m= .
(3)函数y=2※x(x≠0)的图象大致是( )

我们新定义一种三角形:两边平方和等于第三边平方的两倍的三角形叫做奇异三角形.
(1)根据“奇异三角形”的定义,请你判断命题“等边三角形一定是奇异三角形”是真命题还是假命题?
(2)在Rt△ABC中,∠ACB=90°,AB=c,AC=b,BC=a,且b>a,若Rt△ABC是奇异三角形,求a:b:c;
(3)如图,AB是⊙O的直径,C是⊙O上一点(不与点A,B重合),D是半圆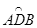 的中点,C,D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.
的中点,C,D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.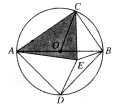
①求证:△ACE是奇异三角形;
②当△ACE是直角三角形时,求∠AOC的度数.
阅读理解:对于任意正实数a、b,∵( -
- )2≥0,∴a-2
)2≥0,∴a-2 +b≥0,∴a+b≥2
+b≥0,∴a+b≥2 ,只有当a=b时,等号成立.
,只有当a=b时,等号成立.
结论:在a+b≥2 (a、b均为正实数)中,若ab为定值p,则a+b≥2
(a、b均为正实数)中,若ab为定值p,则a+b≥2 ,只有当a=b时,a+b有最小值2
,只有当a=b时,a+b有最小值2 . 根据上述内容,回答下列问题:
. 根据上述内容,回答下列问题:
(1)若m>0,只有当m= 时,m+ 有最小值 ;
有最小值 ;
若m>0,只有当m= 时,2m+ 有最小值 .
有最小值 .
(2)如图,已知直线L1:y= x+1与x轴交于点A,过点A的另一直线L2与双曲线y=
x+1与x轴交于点A,过点A的另一直线L2与双曲线y= (x>0)相交于点B(2,m),求直线L2的解析式.
(x>0)相交于点B(2,m),求直线L2的解析式.

(3)在(2)的条件下,若点C为双曲线上任意一点,作CD∥y轴交直线L1于点D,试求当线段CD最短时,点A、B、C、D围成的四边形面积.
如图是一组密码的一部分.为了保密,许多情况下可采用不同的密码,请你运用所学知识找到破译的“钥匙”。目前,已破译出“正做数学”的真实意思是“祝你成功”。若“正”所处的位置为(x,y),你找到的密码钥匙是 ,破译的“今天考试”真实意思是 。

对于实数x,我们规定 表示不大于x的最大整数,如
表示不大于x的最大整数,如 ,现对82进行如下操作:
,现对82进行如下操作: ,这样对82只需进行3次操作后变为1,类似地,①对121只需进行 次操作后变为1;②只需进行3次操作后变为1的所有正整数中,最大的是 .
,这样对82只需进行3次操作后变为1,类似地,①对121只需进行 次操作后变为1;②只需进行3次操作后变为1的所有正整数中,最大的是 .
初三年级某班有54名学生,所在教室有6行9列座位,用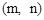 表示第
表示第 行第
行第 列的座位,新学期准备调整座位,设某个学生原来的座位为
列的座位,新学期准备调整座位,设某个学生原来的座位为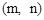 ,如果调整后的座位为
,如果调整后的座位为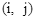 ,则称该生作了平移
,则称该生作了平移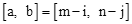 ,并称
,并称 为该生的位置数。若当
为该生的位置数。若当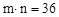 时,
时, 取得最小值,则该生位置数的最大值为 。
取得最小值,则该生位置数的最大值为 。
阅读下列文字与例题
将一个多项式分组后,可提公因式或运用公式继续分解的方法是分组分解法。
例如:(1) ,
,
(2)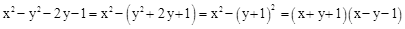 。
。
试用上述方法分解因式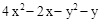 。
。
 是闭区间[1,2014]上的“闭函数”吗?请判断并说明理由;
是闭区间[1,2014]上的“闭函数”吗?请判断并说明理由; 是闭区间[m,n]上的“闭函数”,求此函数的解析式;
是闭区间[m,n]上的“闭函数”,求此函数的解析式; 是闭区间[a,b]上的“闭函数”,求实数a,b的值.
是闭区间[a,b]上的“闭函数”,求实数a,b的值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号