初中数学反比例函数的性质试题

如图，点 $P$ 为函数 $y=\frac{1}{2}x+1$ 与函数 $y=\frac{m}{x}(x>0)$ 图象的交点，点 $P$ 的纵坐标为4， $\mathit{PB}\perp x$ 轴，垂足为点 $B$ ．

（1）求 $m$ 的值；

（2）点 $M$ 是函数 $y=\frac{m}{x}(x>0)$ 图象上一动点，过点 $M$ 作 $\mathit{MD}\perp \mathit{BP}$ 于点 $D$ ，若 $\tan \angle \mathit{PMD}=\frac{1}{2}$ ，求点 $M$ 的坐标．

从 $-1$，2， $-3$，4这四个数中任取两个不同的数分别作为 $a$， $b$的值，得到反比例函数 $y=\frac{\mathit{ab}}{x}$，则这些反比例函数中，其图象在二、四象限的概率是　　．

已知点 $A（x_1，y_1）$， $B（x_2，y_2）$在反比例函数 $y\mathit{＝﹣}\frac{3}{x}$的图象上，若 $y_1＜y_2＜0$，则下列结论正确的是（　　）

A． $x_1＜x_2＜0$B． $x_2＜x_1＜0$C． $0＜x_1＜x_2$D． $0＜x_2＜x_1$

根据反比例函数的性质、联系化学学科中的溶质质量分数的求法以及生活体验等，判定下列有关函数 $y=\frac{x}{a+x}(a$ 为常数且 $a>0$ ， $x>0)$ 的性质表述中，正确的是 $($ 　　 $)$

① $y$ 随 $x$ 的增大而增大

② $y$ 随 $x$ 的增大而减小

③ $0<y<1$

④ $0⩽y⩽1$

A．

①③

B．

①④

C．

②③

D．

②④

已知点 $(-2$， $a\left)\right(2$， $b\left)\right(3$， $c)$在函数 $y=\frac{k}{x}(k>0)$的图象上，则下列判断正确的是 $($　　 $)$

A． $a<b<c$B． $b<a<c$C． $a<c<b$D． $c<b<a$

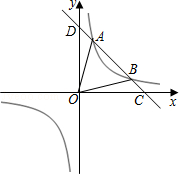
如图，在平面直角坐标系 $\mathit{xOy}$中，一次函数 $y＝\mathit{ax}+b（a\ne 0）$的图象与反比例函数 $y=\frac{k}{x}（k\ne 0，x＞0）$的图象相交于 $A（1，5）$， $B（m，1）$两点，与x轴，y轴分别交于点C，D，连接OA，OB．

（1）求反比例函数 $y=\frac{k}{x}（k\ne 0，x＞0）$和一次函数 $y＝\mathit{ax}+b（a\ne 0）$的表达式；

（2）求 $△\mathit{AOB}$的面积．

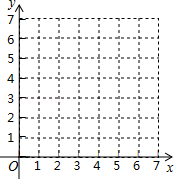
经过实验获得两个变量 $x(x>0)$， $y(y>0)$的一组对应值如下表．

$x$	1	2	3	4	5	6
$y$	6	2.9	2	1.5	1.2	1

（1）请画出相应函数的图象，并求出函数表达式．

（2）点 $A(x_1$， $y_1)$， $B(x_2$， $y_2)$在此函数图象上．若 $x_1<x_2$，则 $y_1$， $y_2$有怎样的大小关系？请说明理由．

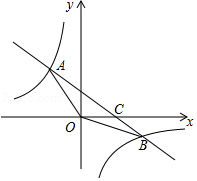
如图，在直角坐标系中，直线 $y_1=\mathit{ax}+b$与双曲线 $y_2=\frac{k}{x}(k\ne 0)$分别相交于第二、四象限内的 $A(m,4)$， $B(6,n)$两点，与 $x$轴相交于 $C$点．已知 $\mathit{OC}=3$， $\tan \angle \mathit{ACO}=\frac{2}{3}$．

（1）求 $y_1$， $y_2$对应的函数表达式；

（2）求 $\mathit{\Delta AOB}$的面积；

（3）直接写出当 $x<0$时，不等式 $\mathit{ax}+b>\frac{k}{x}$的解集．

如图，一次函数 $y=k_{1}x+b(k_1\ne 0)$ 与反比例函数 $y=\frac{k_2}{x}(k_2\ne 0)$ 的图象交于点 $A(2,3)$ ， $B(n,-1)$ ．

（1）求反比例函数和一次函数的解析式；

（2）判断点 $P(-2,1)$ 是否在一次函数 $y=k_{1}x+b$ 的图象上，并说明理由；

（3）写出不等式 $k_{1}x+b⩾\frac{k_2}{x}$ 的解集．

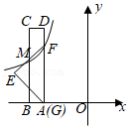
如图，将一把矩形直尺 $\mathit{ABCD}$和一块等腰直角三角板 $\mathit{EFG}$摆放在平面直角坐标系中， $\mathit{AB}$在 $x$轴上，点 $G$与点 $A$重合，点 $F$在 $\mathit{AD}$上， $\mathit{EF}$交 $\mathit{BC}$于点 $M$，反比例函数 $y=\frac{k}{x}(x<0)$的图象恰好经过点 $F$， $M$，若直尺的宽 $\mathit{CD}=1$，三角板的斜边 $\mathit{FG}=4$，则 $k=$　　．

在反比例函数 $y=\frac{k^2+1}{x}(k$ 为常数）上有三点 $A(x_1$ ， $y_1)$ ， $B(x_2$ ， $y_2)$ ， $C(x_3$ ， $y_3)$ ，若 $x_1<0<x_2<x_3$ ，则 $y_1$ ， $y_2$ ， $y_3$ 的大小关系为 $($ 　　 $)$

A．

$y_1<y_2<y_3$

B．

$y_2<y_1<y_3$

C．

$y_1<y_3<y_2$

D．

$y_3<y_2<y_1$

已知三个点 $(x_1$ ， $y_1)$ ， $(x_2$ ， $y_2)$ ， $(x_3$ ， $y_3)$ 在反比例函数 $y=\frac{2}{x}$ 的图象上，其中 $x_1<x_2<0<x_3$ ，下列结论中正确的是 $($ 　　 $)$

A．

$y_2<y_1<0<y_3$

B．

$y_1<y_2<0<y_3$

C．

$y_3<0<y_2<y_1$

D．

$y_3<0<y_1<y_2$

关于某个函数表达式，甲、乙、丙三位同学都正确地说出了该函数的一个特征．

甲：函数图象经过点 $(-1,1)$ ；

乙：函数图象经过第四象限；

丙：当 $x>0$ 时， $y$ 随 $x$ 的增大而增大．

则这个函数表达式可能是 $($ 　　 $)$

A．

$y=-x$

B．

$y=\frac{1}{x}$

C．

$y=x^2$

D．

$y=-\frac{1}{x}$

若点 $A(-5,y_1)$ ， $B(1,y_2)$ ， $C(5,y_3)$ 都在反比例函数 $y=-\frac{5}{x}$ 的图象上，则 $y_1$ ， $y_2$ ， $y_3$ 的大小关系是 $($ 　　 $)$

A．

$y_1<y_2<y_3$

B．

$y_2<y_3<y_1$

C．

$y_1<y_3<y_2$

D．

$y_3<y_1<y_2$

如图，在平面直角坐标系 $\mathit{xOy}$ 中，一次函数 $y=\frac{1}{2}x+b$ 的图象分别与 $x$ 轴、 $y$ 轴交于点 $A$ 、 $B$ ，与反比例函数 $y=\frac{k}{x}(x>0)$ 的图象交于点 $C$ ，连接 $\mathit{OC}$ ．已知点 $A(-4,0)$ ， $\mathit{AB}=2\mathit{BC}$ ．

（1）求 $b$ 、 $k$ 的值；

（2）求 $\mathit{\Delta AOC}$ 的面积．