某市推出电脑上网包月制,每月收取费用 (元 与上网时间 (小时)的函数关系如图所示,其中 是线段,且 轴, 是射线.
(1)当 ,求 与 之间的函数关系式;
(2)若小李4月份上网20小时,他应付多少元的上网费用?
(3)若小李5月份上网费用为75元,则他在该月份的上网时间是多少?

“五 一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游.
根据以下信息,解答下列问题:
(1)设租车时间为 小时,租用甲公司的车所需费用为 元,租用乙公司的车所需费用为 元,分别求出 , 关于 的函数表达式;
(2)请你帮助小明计算并选择哪个出游方案合算.

某市规定了每月用水18立方米以内(含18立方米)和用水18立方米以上两种不同的收费标准.该市的用户每月应交水费 (元 是用水量 (立方米)的函数,其图象如图所示.
(1)若某月用水量为18立方米,则应交水费多少元?
(2)求当 时, 关于 的函数表达式,若小敏家某月交水费81元,则这个月用水量为多少立方米?

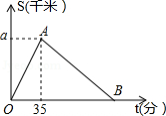
2016年3月27日“丽水半程马拉松竞赛”在莲都举行,某运动员从起点万地广场西门出发,途经紫金大桥,沿比赛路线跑回终点万地广场西门.设该运动员离开起点的路程 (千米)与跑步时间 (分钟)之间的函数关系如图所示,其中从起点到紫金大桥的平均速度是0.3千米 分,用时35分钟,根据图象提供的信息,解答下列问题:
(1)求图中 的值;
(2)组委会在距离起点2.1千米处设立一个拍摄点 ,该运动员从第一次经过 点到第二次经过 点所用的时间为68分钟.
①求 所在直线的函数解析式;
②该运动员跑完赛程用时多少分钟?

2016年3月27日“丽水半程马拉松竞赛”在莲都举行,某运动员从起点万地广场西门出发,途经紫金大桥,沿比赛路线跑回终点万地广场西门.设该运动员离开起点的路程 (千米)与跑步时间 (分钟)之间的函数关系如图所示,其中从起点到紫金大桥的平均速度是0.3千米 分,用时35分钟,根据图象提供的信息,解答下列问题:
(1)求图中 的值;
(2)组委会在距离起点2.1千米处设立一个拍摄点 ,该运动员从第一次经过 点到第二次经过 点所用的时间为68分钟.
①求 所在直线的函数解析式;
②该运动员跑完赛程用时多少分钟?
如图1表示同一时刻的韩国首尔时间和北京时间,两地时差为整数.
(1)设北京时间为 (时 ,首尔时间为 (时 ,就 ,求 关于 的函数表达式,并填写下表(同一时刻的两地时间).
北京时间 |
|
|
|
首尔时间 |
|
|
|
(2)如图2表示同一时刻的英国伦敦时间(夏时制)和北京时间,两地时差为整数.如果现在伦敦(夏时制)时间为 ,那么此时韩国首尔时间是多少?

根据卫生防疫部门要求,游泳池必须定期换水,清洗.某游泳池周五早上 打开排水孔开始排水,排水孔的排水速度保持不变,期间因清洗游泳池需要暂停排水,游泳池的水在 全部排完.游泳池内的水量 和开始排水后的时间 之间的函数图象如图所示,根据图象解答下列问题:
(1)暂停排水需要多少时间?排水孔排水速度是多少?
(2)当 时,求 关于 的函数表达式.

随着某市养老机构(养老机构指社会福利院、养老院、社区养老中心等)建设稳步推进,拥有的养老床位不断增加.
(1)该市的养老床位数从2013年底的2万个增长到2015年底的2.88万个,求该市这两年(从2013年度到2015年底)拥有的养老床位数的平均年增长率;
(2)若该市某社区今年准备新建一养老中心,其中规划建造三类养老专用房间共100间,这三类养老专用房间分别为单人间 个养老床位),双人间 个养老床位),三人间 个养老床位),因实际需要,单人间房间数在10至30之间(包括10和 ,且双人间的房间数是单人间的2倍,设规划建造单人间的房间数为 .
①若该养老中心建成后可提供养老床位200个,求 的值;
②求该养老中心建成后最多提供养老床位多少个?最少提供养老床位多少个?
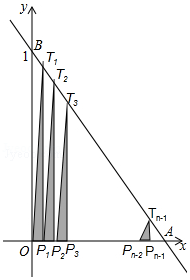
如图,直线 与两坐标轴分别交于 , 两点,将线段 分成 等份,分点分别为 , , , , ,过每个分点作 轴的垂线分别交直线 于点 , , , , ,用 , , , , 分别表示 △ , △ , , △ 的面积,则 .
某商场计划购进 , 两种型号的手机,已知每部 型号手机的进价比每部 型号手机进价多500元,每部 型号手机的售价是2500元,每部 型号手机的售价是2100元.商场用50000元共购进 型号手机10部, 型号手机20部.
(1)求 、 两种型号的手机每部进价各是多少元?
(2)为了满足市场需求,商场决定用不超过7.5万元采购 、 两种型号的手机共40部,且 型号手机的数量不少于 型号手机数量的2倍.
①该商场有哪几种进货方式?
②该商场选择哪种进货方式,获得的利润最大?
某销售商准备在南充采购一批丝绸,经调查,用10000元采购 型丝绸的件数与用8000元采购 型丝绸的件数相等,一件 型丝绸进价比一件 型丝绸进价多100元.
(1)求一件 型、 型丝绸的进价分别为多少元?
(2)若销售商购进 型、 型丝绸共50件,其中 型的件数不大于 型的件数,且不少于16件,设购进 型丝绸 件.
①求 的取值范围.
②已知 型的售价是800元 件,销售成本为 元 件; 型的售价为600元 件,销售成本为 元 件.如果 ,求销售这批丝绸的最大利润 (元 与 (元 的函数关系式(每件销售利润 售价 进价 销售成本).
某车行去年 型车的销售总额为6万元,今年每辆车的售价比去年减少400元.若卖出的数量相同,销售总额将比去年减少 .
(1)求今年 型车每辆车的售价.
(2)该车行计划新进一批 型车和 型车共45辆,已知 、 型车的进货价格分别是1100元、1400元,今年 型车的销售价格是2000元,要求 型车的进货数量不超过 型车数量的两倍,应如何进货才能使这批车获得最大利润,最大利润是多少?
为了美化环境,建设宜居成都,我市准备在一个广场上种植甲、乙两种花卉,经市场调查,甲种花卉的种植费用 (元 与种植面积 之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.
(1)直接写出当 和 时, 与 的函数关系式;
(2)广场上甲、乙两种花卉的种植面积共 ,若甲种花卉的种植面积不少于 ,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植总费用最少?最少总费用为多少元?

学校需要添置教师办公桌椅 、 两型共200套,已知2套 型桌椅和1套 型桌椅共需2000元,1套 型桌椅和3套 型桌椅共需3000元.
(1)求 , 两型桌椅的单价;
(2)若需要 型桌椅不少于120套, 型桌椅不少于70套,平均每套桌椅需要运费10元.设购买 型桌椅 套时,总费用为 元,求 与 的函数关系式,并直接写出 的取值范围;
(3)求出总费用最少的购置方案.