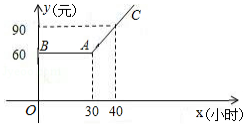
某市推出电脑上网包月制，每月收取费用 （元 与上网时间 （小时）的函数关系如图所示，其中 是线段，且 轴， 是射线．
（1）当 ，求 与 之间的函数关系式；
（2）若小李4月份上网20小时，他应付多少元的上网费用？
（3）若小李5月份上网费用为75元，则他在该月份的上网时间是多少？
相关试题
虹承中学为做好学生“午餐工程”工作，学校工作人员搭配了A，B，C，D四种不同种类的套餐，学校决定围绕“在A，B，C，D四种套餐中，你最喜欢的套餐种类是什么?
(必选且只选一种)”的问题，在全校范围内随机抽取部分学生进行问卷调查，将调查问适当整理后绘制成如图所示的不完整的条形统计图，其中最喜欢D种套餐的学生占被抽取人数的20％．
请你根据以上信息解答下列问题：
（1）在这次调查中，一共抽取了多少名学生?
（2）通过计算，补全条形统计图；
（3）如果全校有2 000名学生．请你估计全校学生中最喜欢B种套餐的学生有多少名?
小磊要制作一个三角形的钢架模型，在这个三角形中，长度为x(单位：cm)的边与这条边上的高之和为40 cm，这个三角形的面积S(单位：cm2)随x(单位：cm)的变化而变化．
（1）请直接写出S与x之间的函数关系式(不要求写出自变量x的取值范围)；
（2）当x是多少时，这个三角形面积S最大?最大面积是多少?
图l、图2是两张形状、大小完全相同的方格纸，方格纸中的每个小正方形的边长均为1．点A和点B在小正方形的顶点上．
（1）在图1中画出△ABC(点C在小正方形的顶点上)，使△ABC为直角三角形(画一个 即可)；
（2）在图2中画出△ABD(点D在小正方形的顶点上)，使△ABD为等腰三角形(画一个即可)；
cos300+
相关知识点
推荐套卷
粤公网安备 44130202000953号