2017年遂宁市吹响了全国文明城市创建决胜“集结号”.为了加快创建步伐,某运输公司承担了某标段的土方运输任务,公司已派出大小两种型号的渣土运输车运输土方.已知一辆大型渣土运输车和一辆小型渣土运输车每次共运15吨;3辆大型渣土运输车和8辆小型渣土运输车每次共运70吨.
(1)一辆大型渣土运输车和一辆小型渣土运输车每次各运土方多少吨?
(2)该渣土运输公司决定派出大小两种型号渣土运输车共20辆参与运输土方,若每次运输土方总量不小于148吨,且小型渣土运输车至少派出7辆,问该渣土运输公司有几种派出方案?
(3)在(2)的条件下,已知一辆大型渣土运输车运输花费500元 次,一辆小型渣土运输车运输花费300元 次,为了节约开支,该公司应选择哪种方案划算?
攀枝花芒果由于品质高、口感好而闻名全国,通过优质快捷的网络销售渠道,小明的妈妈先购买了2箱 品种芒果和3箱 品种芒果,共花费450元;后又购买了1箱 品种芒果和2箱 品种芒果,共花费275元(每次两种芒果的售价都不变).
(1)问 品种芒果和 品种芒果的售价分别是每箱多少元?
(2)现要购买两种芒果共18箱,要求 品种芒果的数量不少于 品种芒果数量的2倍,但不超过 品种芒果数量的4倍,请你设计购买方案,并写出所需费用最低的购买方案.
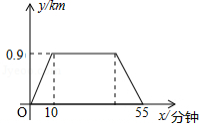
小明从家到图书馆看报然后返回,他离家的距离 与离家的时间 之间的对应关系如图所示,如果小明在图书馆看报30分钟,那么他离家50分钟时离家的距离为 .
江南农场收割小麦,已知1台大型收割机和3台小型收割机1小时可以收割小麦1.4公顷,2台大型收割机和5台小型收割机1小时可以收割小麦2.5公顷.
(1)每台大型收割机和每台小型收割机1小时收割小麦各多少公顷?
(2)大型收割机每小时费用为300元,小型收割机每小时费用为200元,两种型号的收割机一共有10台,要求2小时完成8公顷小麦的收割任务,且总费用不超过5400元,有几种方案?请指出费用最低的一种方案,并求出相应的费用.
为落实“绿水青山就是金山银山”的发展理念,某市政部门招标一工程队负责在山脚下修建一座水库的土方施工任务.该工程队有 , 两种型号的挖掘机,已知3台 型和5台 型挖掘机同时施工一小时挖土165立方米;4台 型和7台 型挖掘机同时施工一小时挖土225立方米.每台 型挖掘机一小时的施工费用为300元,每台 型挖掘机一小时的施工费用为180元.
(1)分别求每台 型, 型挖掘机一小时挖土多少立方米?
(2)若不同数量的 型和 型挖掘机共12台同时施工4小时,至少完成1080立方米的挖土量,且总费用不超过12960元,问施工时有哪几种调配方案,并指出哪种调配方案的施工费用最低,最低费用是多少元?
“绿水青山就是金山银山”,随着生活水平的提高,人们对饮水品质的需求越来越高,孝感市槐荫公司根据市场需求代理 , 两种型号的净水器,每台 型净水器比每台 型净水器进价多200元,用5万元购进 型净水器与用4.5万元购进 型净水器的数量相等.
(1)求每台 型、 型净水器的进价各是多少元?
(2)槐荫公司计划购进 , 两种型号的净水器共50台进行试销,其中 型净水器为 台,购买资金不超过9.8万元.试销时 型净水器每台售价2500元, 型净水器每台售价2180元,槐荫公司决定从销售 型净水器的利润中按每台捐献 元作为公司帮扶贫困村饮水改造资金,设槐荫公司售完50台净水器并捐献扶贫资金后获得的利润为 ,求 的最大值.
甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离 (米)与甲出发的时间 (分)之间的关系如图所示,下列结论:
①甲步行的速度为60米 分;
②乙走完全程用了32分钟;
③乙用16分钟追上甲;
④乙到达终点时,甲离终点还有300米.
其中正确的结论有

A.1个B.2个C.3个D.4个
用1块 型钢板可制成2块 型钢板和1块 型钢板;用1块 型钢板可制成1块 型钢板和3块 型钢板.现准备购买 、 型钢板共100块,并全部加工成 、 型钢板.要求 型钢板不少于120块, 型钢板不少于250块,设购买 型钢板 块 为整数).
(1)求 、 型钢板的购买方案共有多少种?
(2)出售 型钢板每块利润为100元, 型钢板每块利润为120元.若将 、 型钢板全部出售,请你设计获利最大的购买方案.
为了推进我州校园篮球运动的发展,2017年四川省中小学生男子篮球赛于2月在西昌成功举办.在此期间,某体育文化用品商店计划一次性购进篮球和排球共60个,其进价与售价间的关系如下表:
篮球 |
排球 |
|
进价(元 个) |
80 |
50 |
售价(元 个) |
105 |
70 |
(1)商店用4200元购进这批篮球和排球,求购进篮球和排球各多少个?
(2)设商店所获利润为 (单位:元),购进篮球的个数为 (单位:个),请写出 与 之间的函数关系式(不要求写出 的取值范围);
(3)若要使商店的进货成本在4300元的限额内,且全部销售完后所获利润不低于1400元,请你列举出商店所有进货方案,并求出最大利润是多少?
某年5月,我国南方某省 、 两市遭受严重洪涝灾害,1.5万人被迫转移,邻近县市 、 获知 、 两市分别急需救灾物资200吨和300吨的消息后,决定调运物资支援灾区.已知 市有救灾物资240吨, 市有救灾物资260吨,现将这些救灾物资全部调往 、 两市.已知从 市运往 、 两市的费用分别为每吨20元和25元,从 市运往 、 两市的费用别为每吨15元和30元,设从 市运往 市的救灾物资为 吨.
(1)请填写下表
(吨) |
(吨) |
合计(吨) |
|
(吨) |
|
|
240 |
(吨) |
|
|
260 |
总计(吨) |
200 |
300 |
500 |
(2)设 、 两市的总运费为 元,求 与 之间的函数关系式,并写出自变量 的取值范围;
(3)经过抢修,从 市到 市的路况得到了改善,缩短了运输时间,运费每吨减少 元 ,其余路线运费不变.若 、 两市的总运费的最小值不小于10320元,求 的取值范围.
某学校为改善办学条件,计划采购 、 两种型号的空调,已知采购3台 型空调和2台 型空调,需费用39000元;4台 型空调比5台 型空调的费用多6000元.
(1)求 型空调和 型空调每台各需多少元;
(2)若学校计划采购 、 两种型号空调共30台,且 型空调的台数不少于 型空调的一半,两种型号空调的采购总费用不超过217000元,该校共有哪几种采购方案?
(3)在(2)的条件下,采用哪一种采购方案可使总费用最低,最低费用是多少元?
甲、乙两家商场平时以同样价格出售相同的商品.新冠疫情期间,为了减少库存,甲、乙两家商场打折促销.甲商场所有商品按9折出售,乙商场对一次购物中超过100元后的价格部分打8折.
(1)以 (单位:元)表示商品原价, (单位:元)表示实际购物金额,分别就两家商场的让利方式写出 关于 的函数解析式;
(2)新冠疫情期间如何选择这两家商场去购物更省钱?
“和谐号”火车从车站出发,在行驶过程中速度 (单位: 与时间 (单位: 的关系如图所示,其中线段 轴.
请根据图象提供的信息解答下列问题:
(1)当 ,求 关于 的函数解析式;
(2)求 点的坐标.

为满足社区居民健身的需要,市政府准备采购若干套健身器材免费提供给社区,经考察,劲松公司有 , 两种型号的健身器材可供选择.
(1)劲松公司2015年每套 型健身器材的售价为2.5万元,经过连续两年降价,2017年每套售价为1.6万元,求每套 型健身器材年平均下降率 ;
(2)2017年市政府经过招标,决定年内采购并安装劲松公司 , 两种型号的健身器材共80套,采购专项经费总计不超过112万元,采购合同规定:每套 型健身器材售价为1.6万元,每套 型健身器材售价为 万元.
① 型健身器材最多可购买多少套?
②安装完成后,若每套 型和 型健身器材一年的养护费分别是购买价的 和 ,市政府计划支出10万元进行养护,问该计划支出能否满足一年的养护需要?
某公司开发出一款新的节能产品,该产品的成本价为6元 件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试销售,售价为8元 件,工作人员对销售情况进行了跟踪记录,并将记录情况绘成图象,图中的折线 表示日销售量 (件)与销售时间 (天)之间的函数关系,已知线段 表示的函数关系中,时间每增加1天,日销售量减少5件.
(1)第24天的日销售量是 件,日销售利润是 元.
(2)求 与 之间的函数关系式,并写出 的取值范围;
(3)日销售利润不低于640元的天数共有多少天?试销售期间,日销售最大利润是多少元?
