初中数学规律型：数字的变化类试题

杨辉三角，又称贾宪三角，是二项式系数在三角形中的一种几何排列，如图，观察下面的杨辉三角：

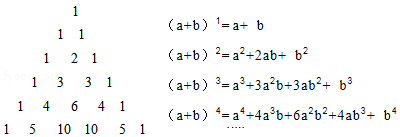
按照前面的规律，则 ${(a+b)}^5=$　　．

我国古代数学的许多创新和发展都位居世界前列，如南宋数学家杨辉（约13世纪）所著的《详解九章算术》一书中，用如图的三角形解释二项式 ${(a+b)}^n$的展开式的各项系数，此三角形称为“杨辉三角”．

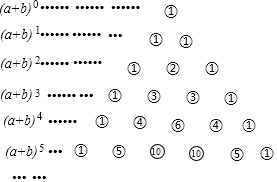
根据“杨辉三角”请计算 ${(a+b)}^{20}$的展开式中第三项的系数为 $($　　 $)$

A．2017B．2016C．191D．190

观察下列运算过程：

计算： $1+2+2^2+\dots +2^{10}$．

解：设 $S=1+2+2^2+\dots +2^{10}$，①

① $\times 2$得

$2S=2+2^2+2^3+\dots +2^{11}$，② $?$

② $-$①得

$S=2^{11}-1$．

所以， $1+2+2^2+\dots +2^{10}=2^{11}-1$

运用上面的计算方法计算： $1+3+3^2+\dots +3^{2017}=$　　．

阅读材料并解决问题：

求 $1+2+2^2+2^3+\dots +2^{2014}$的值，令 $S=1+2+2^2+2^3+\dots +2^{2014}$

                  等式两边同时乘以2，则 $2S=2+2^2+2^3+\dots +2^{2014}+2^{2015}$

                  两式相减：得 $2S-S=2^{2015}-1$

                  所以， $S=2^{2015}-1$

依据以上计算方法，计算 $1+3+3^2+3^3+\dots +3^{2015}=$　　．

按一定规律排列的一列数依次为：2，3，10，15，26，35， $\dots$，按此规律排列下去，则这列数中的第100个数是 $($　　 $)$

A．9999B．10000C．10001D．10002

计算 $\frac{1}{1\times 3}+\frac{1}{3\times 5}+\frac{1}{5\times 7}+\frac{1}{7\times 9}+\dots +\frac{1}{37\times 39}$的结果是 $($　　 $)$

A． $\frac{19}{37}$B． $\frac{19}{39}$C． $\frac{37}{39}$D． $\frac{38}{39}$

$a_1$， $a_2$， $a_3$， $a_4$， $a_5$， $a_6$， $\dots$，是一列数，已知第1个数 $a_1=4$，第5个数 $a_5=5$，且任意三个相邻的数之和为15，则第2019个数 $a_{2019}$的值是　　．

观察一列数： $-3$，0，3，6，9，12， $\dots$，按此规律，这一列数的第21个数是　　．

将一组数 $\sqrt{2}$，2， $\sqrt{6}$， $2\sqrt{2}$， $\sqrt{10}$， $\dots$， $2\sqrt{10}$，按下列方式进行排列：

$\sqrt{2}$，2， $\sqrt{6}$， $2\sqrt{2}$， $\sqrt{10}$；

$2\sqrt{3}$， $\sqrt{14}$，4， $3\sqrt{2}$， $2\sqrt{5}$；

$\dots$

若2的位置记为 $(1,2)$， $2\sqrt{3}$的位置记为 $(2,1)$，则 $\sqrt{38}$这个数的位置记为 $($　　 $)$

A． $(5,4)$B． $(4,4)$C． $(4,5)$D． $(3,5)$

观察以下一列数的特点：0，1， $-4$，9， $-16$，25， $\dots$，则第11个数是 $($　　 $)$

A． $-121$B． $-100$C．100D．121

已知一列数 $a$， $b$， $a+b$， $a+2b$， $2a+3b$， $3a+5b$， $\dots \dots$，按照这个规律写下去，第9个数是　　．

按一定规律排列的一组数： $\frac{1}{2}$， $\frac{1}{6}$， $\frac{1}{12}$， $\frac{1}{20}$， $\dots$， $\frac{1}{a}$， $\frac{1}{90}$， $\frac{1}{b}$（其中 $a$， $b$为整数），则 $a+b$的值为 $($　　 $)$

A．182B．172C．242D．200

设一列数中相邻的三个数依次为 $m$、 $n$、 $p$，且满足 $p=m^2-n$，若这列数为 $-1$，3， $-2$， $a$， $-7$， $b\dots$，则 $b=$　　．

求 $2^1+2^2+2^3+\dots +2^n$的值，解题过程如下：

解：设： $S=2^1+2^2+2^3+\dots +2^n$①

两边同乘以2得： $2S=2^2+2^3+2^4+\dots +2^{n+1}$②

由② $-$①得： $S=2^{n+1}-2$

所以 $2^1+2^2+2^3+\dots +2^n=2^{n+1}-2$

参照上面解法，计算： $1+3^1+3^2+3^3+\dots +3^{n-1}=$　　．

如图所示的三角形数组是我国古代数学家杨辉发现的， 称为杨辉三角形 ． 现用 $A_i$表示第三行开始， 从左往右， 从上往下， 依次出现的第 $i$个数， 例如： $A_1=1$， $A_2=2$， $A_3=1$， $A_4=1$， $A_5=3$， $A_6=3$， $A_7=1$，则 $A_{2016}=$　　．