在平面直角坐标系 中, 的半径为1.对于点 和线段 ,给出如下定义:若将线段 绕点 旋转可以得到 的弦 , 分别是 , 的对应点),则称线段 是 的以点 为中心的“关联线段”.
(1)如图,点 , , , , , , 的横、纵坐标都是整数.在线段 , , 中, 的以点 为中心的“关联线段”是 ;
(2) 是边长为1的等边三角形,点 ,其中 .若 是 的以点 为中心的“关联线段”,求 的值;
(3)在 中, , .若 是 的以点 为中心的“关联线段”,直接写出 的最小值和最大值,以及相应的 长.

如图,一段抛物线:y=﹣x(x﹣3)(0≤x≤3),记为C1,它与x轴交于点O,A1;
将C1绕点A1旋转180°得C2,交x轴于点A2;
将C2绕点A2旋转180°得C3,交x轴于点A3;
…
如此进行下去,直至得C13.若P(37,m)在第13段抛物线C13上,则m= .
这是一个很著名的故事:阿基米德与国王下棋,国王输了,国王问阿基米德要什么奖赏?阿基米德对国王说:“我只要在棋盘上第一格放一粒米,第二格放二粒,第三格放四粒,第四格放十六粒……按这个方法放满整个棋盘就行。”国王以为要不了多少粮食,就随口答应了,结果国王输了.
(1)我们知道,国际象棋共有64个格子,则在第64格中应放多少米?(用幂表示)
(2)请探究第(1)中的数的末位数字是多少?(简要写出探究过程.)
(3)你知道国王输给了阿基米德多少粒米吗?为解决这个问题,我们先来看下面的解题过程:
用分数表示无限循环小数: .
.
解:设 ①.等式两边同时乘以10,得
①.等式两边同时乘以10,得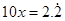 ②.
②.
将②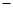 ①得:
①得: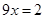 ,则
,则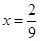 ,∴
,∴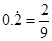 .
.
请参照以上解法求出国王输给阿基米德的米粒数(用幂的形式表示).
抛物线y=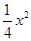 +x+m的顶点在直线y=x+3上,过点F(-2,2)的直线交该抛物线于点M、N两点(点M在点N的左边),MA⊥x轴于点A,NB⊥x轴于点B.
+x+m的顶点在直线y=x+3上,过点F(-2,2)的直线交该抛物线于点M、N两点(点M在点N的左边),MA⊥x轴于点A,NB⊥x轴于点B.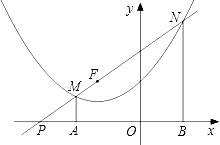
(1)先通过配方求抛物线的顶点坐标(坐标可用含m的代数式表示),再求m的值;
(2)设点N的横坐标为a,试用含a的代数式表示点N的纵坐标,并说明NF=NB;
(3)若射线NM交x轴于点P,且PA•PB=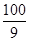 ,求点M的坐标.
,求点M的坐标.
抛物线y=x2+mx+n可以由抛物线y=x2向上平移2个单位,再向左平移3个单位得到,则mn值为()
| A.6 | B.12 | C.54 | D.66 |
一块△ABC余料,已知AB=8cm,BC=15cm,AC=17cm,现将余料裁剪成一个圆形材料,则该圆的最大面积是 .
【提出问题】如图1,小东将一张AD为12,宽AB为4的长方形纸片按如下方式进行折叠:在纸片的一边BC上分别取点P、Q,使得BP=CQ,连结AP、DQ,将△ABP、△DCQ分别沿AP、DQ折叠得△APM,△DQN,连结MN.小东发现线段MN的位置和长度随着点P、Q的位置发生改变.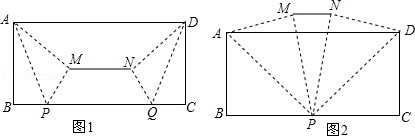
【规律探索】
(1)请在图1中过点M,N分别画ME⊥BC于点E,NF⊥BC于点F.
求证:①ME=NF;②MN∥BC.
【解决问题】
(2)如图1,若BP=3,求线段MN的长;
(3)如图2,当点P与点Q重合时,求MN的长.
小明和小刚做摸纸牌游戏.如图所示,有两组相同的纸牌,每组两张,牌面数字分别是2和3,将两组牌背面朝上,洗匀后从每组牌中各摸出一张,称为一次游戏.当两张牌的牌面数字之积为奇数,小明得2分,否则小刚得1分.这个游戏对双方公平吗?请说明理由.
已知△ABC,以AC为边在△ABC外作等腰△ACD,其中AC=AD.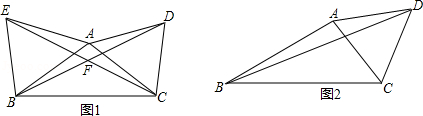
(1)如图1,若AB=AE,∠DAC=∠EAB=60°,求∠BFC的度数;
(2)如图2,∠ABC=α,∠ACD=β,BC=4,BD=6.
①若α=30°,β=60°,AB的长为;
②若改变α,β的大小,但α+β=90°,△ABC的面积是否变化?若不变,求出其值;若变化,说明变化的规律.
如图1,矩形ABCD中,AB=2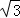 ,BC=6,点P、Q分别是线段AD和线段BC上的动点,满足∠PQB=60°.
,BC=6,点P、Q分别是线段AD和线段BC上的动点,满足∠PQB=60°.
(1)填空:①∠ACB= 度;②PQ= .
(2)设线段BC的中点为N,PQ与线段AC相交于点M,若△CMN为直角三角形,请直接写出满足条件的AP的长度.
(3)设AP=x,△PBQ与△ABC的重叠部分的面积为S,试求S与x的函数关系式和自变量x的取值范围.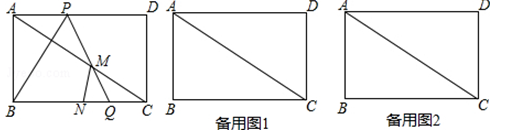
如图,抛物线y=-x2-2x+3 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
(1)求A、B、C的坐标;
(2)点M为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N.若点P在点Q左边,当矩形PMNQ的周长最大时,求△AEM的面积;
(3)在(2)的条件下,当矩形PMNQ的周长最大时,连接DQ.过抛物线上一点F作y轴的平行线,与直线AC交于点G(点G在点F的上方).若FG=2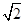 DQ,求点F的坐标.
DQ,求点F的坐标.
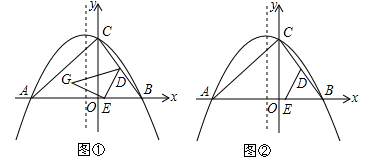
已知,△ABC在平面直角坐标系中的位置如图①所示,A点坐标为(﹣6,0),B点坐标为(4,0),点D为BC的中点,点E为线段AB上一动点,连接DE经过点A、B、C三点的抛物线的解析式为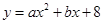 .
.
(1)求抛物线的解析式;
(2)如图①,将△BDE以DE为轴翻折,点B的对称点为点G,当点G恰好落在抛物线的对称轴上时,求G点的坐标;
(3)如图②,当点E在线段AB上运动时,抛物线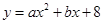 的对称轴上是否存在点F,使得以C、D、E、F为顶点的四边形为平行四边形?若存在,请直接写出点F的坐标;若不存在,请说明理由.
的对称轴上是否存在点F,使得以C、D、E、F为顶点的四边形为平行四边形?若存在,请直接写出点F的坐标;若不存在,请说明理由.
已知,抛物线y=ax2+bx+4(a≠0)与x轴交于A(﹣2,0)、B(8,0)两点,与y轴交于点C.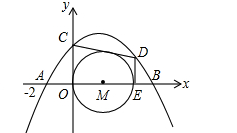
(1)求此抛物线的解析式;
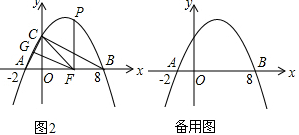
(2)如图1,点E是线段OB上一动点,过点E作DE⊥x轴,交抛物线于点D,若直线CD与以OE为直径的⊙M相切,试求出点E的坐标;
(3)如图2,在抛物线上是否存在一点P,过点P作x轴的垂线,垂足为F,过点F作FG∥BC,交线段AC于点G,连接FC,使△BCF∽△CFG?若存在,求出点P的坐标;若不存在,请说明理由.
如图1,在正方形ABCD中,点E、F分别在边BC、CD上,且BE=DF,点P是AF的中点,点Q是直线AC与EF的交点,连接PQ、PD.
(1)求证:AC垂直平分EF;
(2)试判断△PDQ的形状,并加以证明;
(3)如图2,若将△CEF绕着点C旋转180°,其余条件不变,则(2)中的结论还成立吗?若成立,请加以证明;若不成立,请说明理由.