已知,抛物线y=ax2+bx+4(a≠0)与x轴交于A(﹣2,0)、B(8,0)两点,与y轴交于点C.

(1)求此抛物线的解析式;
(2)如图1,点E是线段OB上一动点,过点E作DE⊥x轴,交抛物线于点D,若直线CD与以OE为直径的⊙M相切,试求出点E的坐标;
(3)如图2,在抛物线上是否存在一点P,过点P作x轴的垂线,垂足为F,过点F作FG∥BC,交线段AC于点G,连接FC,使△BCF∽△CFG?若存在,求出点P的坐标;若不存在,请说明理由.
相关知识点
推荐套卷
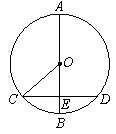
 为原点,点
为原点,点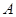 的坐标为
的坐标为  ,点
,点 在第一象限内,
在第一象限内, ,
, .
.
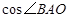 的值.
的值. ,且BD=2,AD=3,求BC的长。
,且BD=2,AD=3,求BC的长。
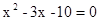
 中,
中, ,
, .分别以
.分别以 所在直线为
所在直线为 轴和
轴和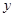 轴,建立如图所示的平面直角坐标系.
轴,建立如图所示的平面直角坐标系. 是边
是边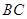 上的一个动点(不与
上的一个动点(不与 重合),过
重合),过 的图象与
的图象与 边交于点
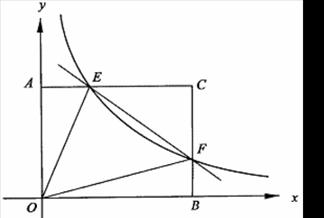
边交于点 .
.
 与
与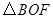 的面积相等;
的面积相等; ,求当
,求当 为何值时,
为何值时,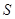 有最大值,最大值为多少
有最大值,最大值为多少 ?
? 沿
沿 对折后,
对折后, 点恰好落在
点恰好落在 上?若存在,求出点
上?若存在,求出点 粤公网安备 44130202000953号
粤公网安备 44130202000953号