高中物理力学实验计算题

如图所示，已知半径分别为R和r的甲、乙两个光滑的圆形轨道安置在同一竖直平面内，甲轨道左侧又连接一个光滑的轨道，两圆形轨道之间由一条水平轨道CD相连．一小球自某一高度由静止滑下，先滑过甲轨道，通过动摩擦因数为μ的CD段，又滑过乙轨道，最后离开.若小球在两圆轨道的最高点对轨道压力都恰好为零．试求：

⑴释放小球的高度h.
⑵水平CD段的长度.

如图，固定在水平面上组合轨道，由光滑的斜面、光滑的竖直半圆(半径R=2.5m)与粗糙的水平轨道组成；水平轨道动摩擦因数μ=0.25，与半圆的最低点相切，轨道固定在水平面上。一个质量为m=0.1kg的小球从斜面上A处静止开始滑下，并恰好能到达半圆轨道最高点D，且水平抛出，落在水平轨道的最左端B点处。不计空气阻力，小球在经过斜面与水平轨道连接处时不计能量损失，g取10m/s²。求：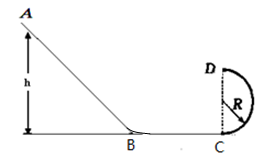

（1）小球出D点的速度v；
（2）水平轨道BC的长度x；
（3）小球开始下落的高度h。

一小孩自己不会荡秋千。爸爸让他坐在秋千板上，将小孩和秋千板一起拉到某一高度，此时绳子与竖直方向的偏角为37°，然后由静止释放。已知小孩的质量为25kg，小孩在最低点时离系绳子的横梁2.5m。重力加速度g=10m/s²。，。忽略秋千的质量，可把小孩看做质点。
（1）假设小孩和秋千受到的阻力可以忽略，当摆到最低点时，求：
a.小孩的速度大小；
b.秋千对小孩作用力的大小。
（2）假设小孩和秋千受到的平均阻力是小孩重力的0.1倍，求从小孩被释放到停止经过的总路程。

如图所示，一个人用一根长为R=1米，能承受最大拉力为F=74N的绳子，系着一个质量为m=1Kg的小球，在竖直平面内作圆周运动，已知圆心O离地面高h=6米。运动中小球在圆周的最低点时绳子刚好被拉断，绳子的质量和空气阻力均忽略不计，g="10" m/s²．求：

（1）绳子被拉断的瞬间，小球的速度v的大小？
（2）绳断后，小球落地点与圆周的最低点间的水平距离x多大？

如图所示，一只标有“8V  4W” 的灯泡L与一只滑动变阻器R串联，开关S闭合，滑动片P在b点时，电压表的示数为12V，灯泡正常发光，当滑动片P从b点滑到a点时，电路中电阻增大了6Ω，

求：（1）灯泡的电阻值及电源电压。
（2）滑动片P在a点时，灯泡的实际功率多大？
（3）你在计算过程中用到了什么近似？

如图所示，光滑半圆形轨道处于竖直平面内，半圆轨道与光滑的水平地面相切于半圆的端点A。一质量为m的小球在水平地面上的C点受水平向左的恒力F由静止开始运动，当运动到A点时撤去恒力F，小球沿竖直半圆轨道运动到轨道最高点B点，最后又落在水平地面上的D点（图中未画出）。已知A、C间的距离为L,重力加速度为g。
（1）若轨道半径为R，求小球到达圆轨道B点时对轨道的压力F_N;
（2）为使小球能运动到轨道最高点B，求轨道半径的最大值R_m；
（3）轨道半径R多大时，小球在水平地面上的落点D到A点的距离最大？最大距离x_m是多少？

电动自行车是一种重要的交通工具，都市中每天有数十万辆电动自行车行驶在大街小巷，形成了一道独特的风景。电动自行车提供能量的装置为装在电池盒内的电池组，当它给电动机供电时，电动机将带动车轮转动。假设有一辆电动自行车，人和车的总质量为120kg。当该车在水平地面上以5m/s的速度匀速行驶时，它受到的阻力约等于人和车总重的0.02倍，此时电池组加在电动机两端的电压为36V，通过电动机的电流为5A。若连接导线的电阻不计，传动装置消耗的能量不计，g取10m/s²。求：
（1）电动机输出的机械功率
（2）电动机线圈的电阻

轻弹簧AB长35cm，A端固定在重50N的物体上，该物体放在倾角为30⁰的斜面上，如图所示，手执B端，使弹簧与斜面平行，当弹簧和物体沿斜面匀速下滑时，弹簧长变为40cm；当弹簧和物体沿斜面匀速上滑时，弹簧长度变为50cm，试求：

（1）求弹簧的劲度系数k；
（2）物体与斜面间的动摩擦因数μ．

如图所示。一端连着质量为m的小球的、长为L的轻杆另一端连在水平光滑轴O上，可在竖直面内转动。当小球运动至最高点A时，杆对小球的支持力大小为mg/2，则当小球运动至最低点B时，杆对小球的拉力大小为多少？

一根轻弹簧，其弹力F的大小与长度x的关系如图的线段a和b所示。求

（1）弹簧原长为多少？
（2）弹簧的劲度系数为多大？
（3）弹簧长度为6cm时，弹力大小为多少？

一劲度系数k="800" N/m的轻质弹簧两端分别连接着质量均为12 kg的物体A、B，将它们竖直静止放在水平面上，如图所示。现将一竖直向上的变力F作用在A上，使A开始向上做匀加速运动，经0.40 s物体B刚要离开地面，取g ="10" m/s²，试求这0.40s内力F所做的功。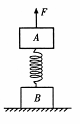

(8分)如图，光滑半圆弧轨道半径为r，OA为水平半径，BC为竖直直径。水平轨道CM与C点相切，轨道上有一轻弹簧，一端固定在竖直墙上，另一端恰位于轨道的末端C点(此时弹簧处于自然状态)。一质量为m的小物块自A处以竖直向下的初速度v₀=滑下，到C点后压缩弹簧进入水平轨道，被弹簧反弹后恰能通过B点。重力加速度为g，求：

(1)物块通过B点时的速度大小；
(2)物块离开弹簧刚进入半圆轨道C点时对轨道的压力大小；
(3)弹簧的最大弹性势能。

蹦床比赛分成预备运动和比赛动作。最初，运动员静止站在蹦床上在预备运动阶段，他经过若干次蹦跳，逐渐增加上升高度，最终达到完成比赛动作所需的高度；此后，进入比赛动作阶段。把蹦床简化为一个竖直放置的轻弹簧，弹力大小F="kx" (x为床面下沉的距离，k为常量)。质量m=50kg的运动员静止站在蹦床上，床面下沉x₀=0.10m；在预备运动中，假设运动员所做的总功W全部用于其机械能；在比赛动作中，把该运动员视作质点，其每次离开床面做竖直上抛运动的腾空时间均为△t=2.0s，设运动员每次落下使床面压缩的最大深度均为x_l。取重力加速度g=I0m/s²，忽略空气阻力的影响。
（1）求常量k，并在图中画出弹力F随x变化的示意图；
（2）求在比赛动作中，运动员离开床面后上升的最大高度h_m;
（3）借助F-x 图像可以确定弹力做功的规律，在此基础上，求 x₁和W的值

如图所示，一人用一根长1m，只能承受46N拉力的绳子，拴着一质量为1kg的小球，在竖直平面内作圆周运动，已知圆心O离地面h＝6m。求：

（1）为使小球能在竖直平面内作完整的圆周运动，小球过最高点时的最小速度为多大？
（2）若在增加转动的速度使小球运动到最低点时绳子恰好断开，则绳子断时小球运动的线速度多大?
（3）绳断后，小球落地点与抛出点间的水平距离。（取＝10m/s²）

如图所示，匀速转动的水平转台上，沿半径方向放置两个用细线相连的小物块A、B（可视为质点），质量分别为kg、kg；细线长m，A、B与转台间的动摩擦因数。开始转动时A放在转轴处，细线刚好拉直但无张力， 重力加速度m/s²。最大静摩擦力等于滑动摩擦力,求：

（1）使细线刚好拉直但无张力，转台转动的最大角速度为多少；
（2）使A、B能随转台一起匀速圆周运动，转台转动的最大角速度为多少