高中物理力学实验计算题

（本题6分）如图所示，水平向右的匀强电场场强为E，有一绝缘轻细杆长为l，一端可绕O点在竖直面内无摩擦转动，另一端粘有一带正电荷的小球，电量为q，质量为m，将小球拉成与O点等高的A点后自由释放，求小球到达最低点B时绝缘杆给小球的力。

在云南省某些地方小学生上学的路上到现在还要依靠滑铁索过江，若把这滑铁索过江简化成如图所示的模型，铁索的两个固定点A、B在同一水平面内，铁索能承受最大压力为2500N，AB间的距离为L=80m，铁索的最低点离AB间的垂直距离为H=8m，若把铁索看做是圆弧，已知一质量m=52kg的人在A处从静止开始借助滑轮（滑轮质量不计）滑到最低点的速度为10m/s。求：
 
（1）从A滑到最低点的过程中阻力做的功？
（2）人在滑到最低点时，滑轮对绳索的压力？
（3）若在A处给人4 m/s的初速度，试判断该同学能不能到达B处？

如图所示，光滑半圆弧轨道半径为r，OA为水平半径，BC为竖直直径。一质量为m 的小物块自A处以某一竖直向下的初速度滑下，进入与C点相切的粗糙水平滑道CM上。在水平滑道上有一轻弹簧，其一端固定在竖直墙上，另一端恰位于滑道的末端C点(此时弹簧处于自然状态)。若物块运动过程中弹簧最大弹性势能为E_p，且物块被弹簧反弹后恰能通过B点。已知物块与水平滑道间的动摩擦因数为μ，重力加速度为g，求：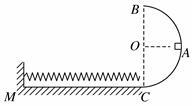

(1)物块被弹簧反弹后恰能通过B点时的速度大小；
(2)物块离开弹簧刚进入半圆轨道c点时对轨道的压力F_N的大小；
(3)物块从A处开始下滑时的初速度大小v₀。

如图甲所示，光滑的水平地面上固定一长L=1.7m的木板C，C板的左端有两个可视为质点的物块A和B，其间夹有一根原长为1.0m、劲度系数k=200N/m的轻弹簧，此时弹簧没有发生形变，且与物块不相连。已知m_A= m_C=20kg，m_B=40kg，A与木板C、B与木板C的动摩擦因数分别为μA=0.50，μB=0.25。假设最大静摩擦力与滑动摩擦力相等。现用水平力F作用于A，让F从零逐渐增大，使A缓慢移动而逐渐压缩弹簧，压缩了一定量后又推动B缓慢地向右移动，当B缓慢向右移动0.5m时，使弹簧储存了弹性势能E₀。（g=10m/s²）问：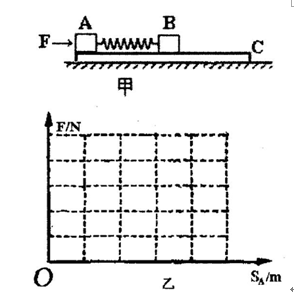

（1）以作用力F为纵坐标，物块A移动的距离为横坐标，试通过定量计算在图乙的坐标系中画出推力F随物块A位移的变化图线。
（2）求出弹簧贮存的弹性势能E₀的大小。
（3）当物块B缓慢地向右移动了0.5m后，保持A、B两物块间距，将其间夹有的弹簧更换，使得压缩量仍相同的新弹簧贮存的弹性势能为12E₀，之后同时释放三物体A、B和C，已被压缩的轻弹簧将A、B向两边弹开，设弹开时A、B两物体的速度之比始终为2：1，求哪一物块先被弹出木板C？最终C的速度是多大？

如图1所示，在某星球表面轻绳约束下的质量为m的小球在竖直平面内做圆周运动，小球在最低点与最高点所受轻绳的拉力之差为ΔF，假设星球是均匀球体，其半径为R，已知万有引力常量为G，不计一切阻力。

（1）求星球表面重力加速度
（2）求该星球的密度
（3）如图所示2，在该星球表面上，某小球以大小为v₀的初速度平抛，恰好能击中倾角为θ的斜面，且位移最短，试求该小球平抛的时间

如图所示，光滑水平面上放置质量均为M＝2 kg的甲、乙两辆小车，两车之间通过一感应开关相连(当滑块滑过感应开关时，两车自动分离)．甲车上表面光滑，乙车上表面与滑块P之间的动摩擦因数μ＝0.5.一根通过细线拴着(细线未画出)且被压缩的轻质弹簧固定在甲车的左端，质量为m＝1 kg的滑块P(可视为质点)与弹簧的右端接触但不相连，此时弹簧的弹性势能E₀＝10 J，弹簧原长小于甲车长度，整个系统处于静止状态．现剪断细线，求：

①滑块P滑上乙车前的瞬时速度的大小．
②滑块P滑上乙车后最终未滑离乙车，滑块P在乙车上滑行的距离．(取g＝10 m/s²)

如图为某工厂生产流水线上水平传输装置的俯视图，它由传送带和转盘组成。物品从A处无初速放到传送带上，运动到B处后进入匀速转动的水平转盘，设物品进入转盘时速度大小不发生变化，此后随转盘一起运动(无相对滑动)到C处被取走装箱。已知A．B两处的距离L＝10 m，传送带的传输速度v＝2 m/s，物品在转盘上与轴O的距离R＝4 m，物品与传送带间的动摩擦因数μ＝0.25。

（1）物品从A处运动到B处的时间t；
（2）质量为2 kg的物品随转盘一起运动的静摩擦力为多大？
（3）在第（2）问中若物品恰好刚能够随转盘一起做匀速圆周运动，试求物品与转盘间的动摩擦因素μ^/（设最大静摩擦力等于滑动摩擦力）

滑板运动是极限运动的鼻祖，许多极限运动项目均由滑板项目延伸而来。如图所示是滑板运动的轨道，BC和DE是两段光滑圆弧形轨道，BC段的圆心为O点，圆心角为60º，半径OC与水平轨道CD垂直，水平轨道CD段粗糙且长8m。一运动员从轨道上的A点以3m/s的速度水平滑出，在B点刚好沿轨道的切线方向滑入圆弧轨道BC，经CD轨道后冲上DE轨道，到达E点时速度减为零，然后返回。已知运动员和滑板的总质量为60kg，B、E两点与水平面CD的竖直高度分别为h和H，且h=2m，H=2.8m，取10m/s²。求：

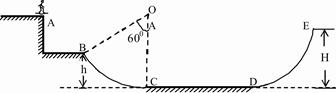
（1）运动员从A运动到达B点时的速度大小v_B；
（2）轨道CD段的动摩擦因数；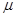
（3）通过计算说明，第一次返回时，运动员能否回到B点？如能，请求出回到B点时速度的大小；如不能，则最后停在何处？

如图所示，轻杆BC的C点用光滑铰链与墙壁固定，杆的B点通过水平细绳AB使杆与竖直墙壁保持30°的夹角．若在B点系一细绳BD，其下端悬挂一质量m=30kg的重物，g取10m/s²．试求：轻杆BC和绳AB所受弹力的大小．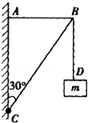

一物块（可视为质点）以4m/s的速度从D点滑上粗糙程度相同的水平地面，途经A、B两点，在A点时的速度是B点时的2倍，由B点再经过0.5s滑到C点时速度减为零，如图所示，A、B相距0.75m．求：
 
(1)D、C的距离；
(2)物块由D点滑到B点所用的时间。

(12分) 如图，等量异种点电荷，固定在水平线上的M、N两点上，有一质量为m、电荷量为＋q（可视为点电荷）的小球，固定在长为L的绝缘轻质细杆的一端，细杆另一端可绕过O点且与MN垂直的水平轴无摩擦地转动，O点位于MN的垂直平分线上距MN为L处。现在把杆拉起到水平位置，由静止释放，小球经过最低点B时速度为v，取O点电势为零，忽略q对等量异种电荷形成电场的影响。求：

(1)小球经过B点时对杆的拉力大小；
(2)在＋Q、－Q形成的电场中，A点的电势φ_A；
(3)小球继续向左摆动，经过与A等高度的C点时的速度大小。

如图所示，已知半径分别为R和r的甲、乙两个光滑的圆形轨道安置在同一竖直平面内，甲轨道左侧又连接一个光滑的轨道，两圆形轨道之间由一条水平轨道CD相连．一小球自某一高度由静止滑下，先滑过甲轨道，通过动摩擦因数为μ的CD段，又滑过乙轨道，最后离开.若小球在两圆轨道的最高点对轨道压力都恰好为零．试求：

⑴释放小球的高度h.
⑵水平CD段的长度.

如图，固定在水平面上组合轨道，由光滑的斜面、光滑的竖直半圆(半径R=2.5m)与粗糙的水平轨道组成；水平轨道动摩擦因数μ=0.25，与半圆的最低点相切，轨道固定在水平面上。一个质量为m=0.1kg的小球从斜面上A处静止开始滑下，并恰好能到达半圆轨道最高点D，且水平抛出，落在水平轨道的最左端B点处。不计空气阻力，小球在经过斜面与水平轨道连接处时不计能量损失，g取10m/s²。求：

（1）小球出D点的速度v；
（2）水平轨道BC的长度x；
（3）小球开始下落的高度h。

一小孩自己不会荡秋千。爸爸让他坐在秋千板上，将小孩和秋千板一起拉到某一高度，此时绳子与竖直方向的偏角为37°，然后由静止释放。已知小孩的质量为25kg，小孩在最低点时离系绳子的横梁2.5m。重力加速度g=10m/s²。，。忽略秋千的质量，可把小孩看做质点。
（1）假设小孩和秋千受到的阻力可以忽略，当摆到最低点时，求：
a.小孩的速度大小；
b.秋千对小孩作用力的大小。
（2）假设小孩和秋千受到的平均阻力是小孩重力的0.1倍，求从小孩被释放到停止经过的总路程。

质量为的带正电小球，电荷量为，通过一根长为的细线系于天花板上，把细线拉直让小球从E点静止释放，由于水平方向电场的存在，使得小球摆过的偏角到达竖直位置时，速度恰好等于0.

（1）求电场强度E；
（2）要小球恰好完成竖直圆周运动，求E点释放小球时应有初速度（可含根式）。