高中物理力学实验计算题

如图所示，半径R =" 0.8" m的光滑绝缘导轨固定于竖直平面内，加上某一方向的匀强电场时，带正电的小球沿轨道内侧做圆周运动。圆心O与A点的连线与竖直成一角度θ，在A点时小球对轨道的压力F_N="120" N，此时小球动能最大。若小球的最大动能比最小动能多32 J，且小球能够到达轨道上的任意一点（不计空气阻力）。则：

⑴小球的最小动能是多少？
⑵小球受到重力和电场力的合力是多少？
⑶现小球在动能最小的位置突然撤去轨道，并保持其他量都不变，若小球在0.04 s后的动能与它在A点时的动能相等，求小球的质量。

如图所示，跨过轻质定滑轮的细绳两端，一端连接质量为m的物体A，另一端通过一轻质弹簧与质量为M的物体B连接，B物体静止在地面上，用手托着A物体，在A距地面高h处时，细绳刚好被拉直、弹簧无形变。今将A物体从h高处无初速释放，A物体恰好能到达地面，且A到达地面时，B物体对地面的压力恰好减为零。已知重力加速度为g，弹簧的弹性势能与劲度系数k、弹簧的伸长量x的关系是：E_弹=kx²。两个物体均可视为质点，不计绳子和滑轮的质量，不计滑轮轴上的摩擦力和空气阻力。问：

（1）A、B两物体的质量之比为多少?
（2）现将A、B两物体的初始位置互换，再让B物体从h高处无初速释放，当A物体刚要离开地面时，B物体的速度是多少?

汽车发动机的额定功率为30KW，质量为1000kg，当汽车在水平路面上行驶时受到阻力为车重的0.1倍()，求：
（1）汽车在路面上能达到的最大速度；
（2）若汽车以额定功率启动，当汽车速度为5m/s时的加速度；
（3）若汽车从静止开始保持2m/s²的加速度作匀加速直线运动，达到额定输出功率后，汽车保持功率不变又加速行驶了200m，直到获得最大速度后才匀速行驶。求汽车从静止到获得最大行驶速度所用的总时间.

(14分)如图所示，光滑圆弧轨道最低点与光滑斜面在B点用一段光滑小圆弧平滑连接，可认为没有能量的损失，圆弧半径为R="0.5" m，斜面的倾角为45⁰，现有一个可视为质点、质量为m="0.1" kg的小球从斜面上A点由静止释放，通过圆弧轨道最低点B时对轨道的压力为6 N。以B点为坐标原点建立坐标系如图所示(g="10" m/s²)。求：

（1）小球最初自由释放位置A离最低点B的高度h；
（2）小球运动到C点时对轨道的压力的大小；
（3）小球从离开C点至第一次落回到斜面上，落点的坐标是多少?

如图所示，一粗糙斜面AB与光滑圆弧轨道BCD相切，C为圆弧轨道的最低点，圆弧BC所对圆心角θ=37°。已知圆弧轨道半径为R＝0.5m，斜面AB的长度为L＝2.875m。质量为m＝1kg的小物块（可视为质点）从斜面顶端A点处由静止开始沿斜面下滑，从B点进入圆弧轨道运动恰能通过最高点D。sin37°＝0.6，cos37°＝0.8，重力加速度g=10m/s²。求：

（1）物块经C点时对圆弧轨道的压力Fc；
（2）物块与斜面间的动摩擦因数μ。

游乐园的小型“摩天轮”上对称站着质量均为m的8位同学，如图所示，“摩天轮”在竖直平面内逆时针匀速转动，若某时刻转到顶点a上的甲同学让一小重物做自由落体运动，并立即通知下面的同学接住，结果重物掉落时正处在c处（如图）的乙同学恰好在第一次到达最低点b处接到，己知“摩天轮”半径为R，重力加速度为g，（不计人和吊篮的大小及重物的质量）．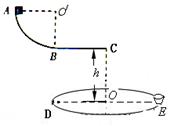


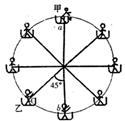
问：（1）接住前重物下落运动的时间t="?" （2）人和吊篮随“摩天轮”运动的线速度大小v=? （3）乙同学在最低点处对地板的压力F_N=?

如图所示，物体在15N的推力F的作用下沿水平地面向右匀速直线运动，已知物体的重力为31N，拉力为F与水平方向的夹角为θ=37°，（sin37°=0.6，cos37°=0.8）问：

（1）物体受到地面的支持力为多大
（2）物体受到的摩擦力为多大
（3）物体与地面的动摩擦因数μ

在许多建筑工地经常使用打夯机将桩料打入泥土中以加固地基。打夯前先将桩料扶起、使其缓慢直立进入泥土中，每次卷扬机都通过滑轮用轻质钢丝绳将夯锤提升到距离桩顶h₀＝5 m处再释放，让夯锤自由下落，夯锤砸在桩料上并不弹起，而随桩料一起向下运动。(碰撞时间极短时,一动碰一静,碰后同速满足mv=(M+m)v_共）设夯锤和桩料的质量均为m＝500 kg，泥土对桩料的阻力为f＝kh，其中常数k＝2. 0×10⁴ N／m，h是桩料深入泥土的深度。卷扬机使用电动机来驱动，卷扬机和电动机总的工作效率为η＝95%，每次卷扬机需用20 s的时间提升夯锤。提升夯锤时忽略加速和减速的过程，不计夯锤提升时的动能，也不计滑轮的摩擦。夯锤和桩料的作用时间极短，g取10m／s²，求：
（1）在提升夯锤的过程中，电动机的输入功率；（结果保留2位有效数字）
（2）打完第一夯后，桩料进入泥土的深度。（可用根号表示）

如图所示，质量为M=0.6kg的物体静止在水平圆形转台上。轻绳的一端系着物体，穿过转台圆心的光滑小孔吊着质量为m=0.3kg的物体，M与小孔的距离为r=0.2m，M与水平面间的动摩擦因数为0.3，现使物体M随转台绕过圆心的竖直轴匀速转动，(g取10m/s²)求：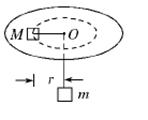

(1)角速度ω为多大时，物体M与平台之间恰好没有摩擦力？
(2)角速度ω=6rad/s时，物体M受到的摩擦力的大小和方向？

如图所示，将小砝码置于桌面上的薄纸板上，用水平向右的拉力将纸板迅速抽出，砝码的移动很小，几乎观察不到，这就是大家熟悉的惯性演示实验．若砝码和纸板的质量分别为m₁和m₂，各接触面间的动摩擦因数均为μ．重力加速度为g．

（1）当纸板相对砝码运动时，求纸板所受摩擦力的大小；
（2）要使纸板相对砝码运动，求所需拉力的大小；
（3）本实验中，m₁=0.5kg，m₂=0.1kg，μ=0.2，砝码与纸板左端的距离d=0.1m，取g=10m/s²．若砝码移动的距离超过l=0.002m，人眼就能感知．为确保实验成功，纸板所需的拉力至少多大？

如图所示，半径R=0.5m的光滑圆环上套有一质量为m=0.1kg的小环，当圆环绕着过环心的竖直轴匀速旋转时，若环每秒钟恰好转过2圈,求小环偏离圆环最低点的高度h。(取g≈π²)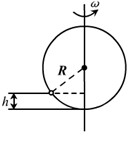

在云南省某些地方小学生上学的路上到现在还要依靠滑铁索过江，若把这滑铁索过江简化成如图所示的模型，铁索的两个固定点A、B在同一水平面内，铁索能承受最大压力为2500N，AB间的距离为L=80m，铁索的最低点离AB间的垂直距离为H=8m，若把铁索看做是圆弧，已知一质量m=52kg的人在A处从静止开始借助滑轮（滑轮质量不计）滑到最低点的速度为10m/s。求：
 
（1）从A滑到最低点的过程中阻力做的功？
（2）人在滑到最低点时，滑轮对绳索的压力？
（3）若在A处给人4 m/s的初速度，试判断该同学能不能到达B处？

如图歼﹣15舰载机成功着陆“辽宁号”航母，设歼﹣15飞机总质量m=2.0×10⁴kg，g=10m/s²．若歼﹣15飞机以V₀=50m/s的水平速度着陆甲板所受其它水平阻力（包括空气和摩擦阻力）恒为10⁵N

（1）飞机着舰后，若仅受水平阻力作用，航母甲板至少多长才能保证飞机不滑到海里？
（2）在阻拦索的作用下，飞机匀减速滑行50m停下，求阻拦索的作用力大小和飞机对飞行员的作用力是飞行员自重的多少倍？
（3）“辽宁号”航母飞行甲板水平，但前端上翘，水平部分与上翘部分平滑连接，连接处D点可看作圆弧上的一点，圆弧半径为R=100m，飞机起飞时速度大容易升空，但也并非越大越好．已知飞机起落架能承受的最大作用力为飞机自重的11倍，求飞机安全起飞经过圆弧处D点的最大速度？

如图所示，物体从光滑斜面上的A点由静止开始匀加速下滑，经过B点后进入水平面（设经过B点前后速度大小不变)，在水平面上做匀减速直线运动，最后停在C点．每隔0.2 s通过速度传感器测量物体的瞬时速度，下表给出了部分测量数据．求：

t（s)	0.0	0.2	0.4	…	1.2	1.4	…
v（m/s)	0.0	1.0	2.0	…	1.1	0.7	…

（1)物体在斜面和水平面上滑行的加速度大小；
（2)物体在斜面上下滑的时间；
（3)t＝0.6 s时的瞬时速度。

如图所示，一个重为100N的小球被夹在竖直的墙壁和A点之间，已知球心O与A点的连线与竖直方向成θ角，且θ=60°，所有接触点和面均不计摩擦．试求小球对墙面的压力F₁和对A点压力F₂．