(14分)如图所示，光滑圆弧轨道最低点与光滑斜面在B点用一段光滑小圆弧平滑连接，可认为没有能量的损失，圆弧半径为R="0.5" m，斜面的倾角为450，现有一个可视为质点、质量为m="0.1" kg的小球从斜面上A点由静止释放，通过圆弧轨道最低点B时对轨道的压力为6 N。以B点为坐标原点建立坐标系如图所示(g="10" m/s2)。求：
（1）小球最初自由释放位置A离最低点B的高度h；
（2）小球运动到C点时对轨道的压力的大小；
（3）小球从离开C点至第一次落回到斜面上，落点的坐标是多少?
相关试题
我校一年一度的田径运动会已经举行。在4×100m接力赛的一组中有甲、乙两位同学，他们在奔跑时具有相同的最大速度。乙从静止开始全力奔跑，需跑出25m才能达到最大速度，这一过程可看做匀变速直线运动。现在甲持棒以最大速度向乙奔来，乙在接力区准备全力奔出。若要求乙接棒时奔跑速度达到最大速度的80%，回答下列问题：乙在接力区必须先跑出多少米？
乙应在距离甲多远时起跑？
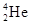）与同方向运动的氖核（
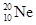）发生弹性正碰，碰后α粒子恰好静止。求碰撞前后氖核的速度（不计相对论修正）。已知某金属表面接受波长为λ和2λ的单色光照射时，释放出光电子的最大初动能分别为30 eV和10 eV，求能使此种金属表面产生光电效应的入射光的极限波长为多少？(λ为未知量)
．氢原子光谱除了巴耳末系外，还有赖曼系、帕邢系等，其中帕邢系的公式为＝
R(－)(n＝4,5,6，…)，R＝1.10×107 m－1.若已知帕邢系的氢原子光谱在红外线区域，试求：
(1)n＝6时，对应的波长；
(2)帕邢系形成的谱线在真空中的波速为多少？n＝6时，传播频率为多大？
相关知识点
粤公网安备 44130202000953号