质量为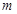 的带正电小球,电荷量为
的带正电小球,电荷量为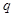 ,通过一根长为
,通过一根长为 的细线系于天花板上,把细线拉直让小球从E点静止释放,由于水平方向电场的存在,使得小球摆过
的细线系于天花板上,把细线拉直让小球从E点静止释放,由于水平方向电场的存在,使得小球摆过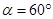 的偏角到达竖直位置时,速度恰好等于0.
的偏角到达竖直位置时,速度恰好等于0.
(1)求电场强度E;
(2)要小球恰好完成竖直圆周运动,求E点释放小球时应有初速度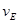 (可含根式)。
(可含根式)。
相关知识点
质量为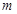 的带正电小球,电荷量为
的带正电小球,电荷量为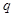 ,通过一根长为
,通过一根长为 的细线系于天花板上,把细线拉直让小球从E点静止释放,由于水平方向电场的存在,使得小球摆过
的细线系于天花板上,把细线拉直让小球从E点静止释放,由于水平方向电场的存在,使得小球摆过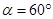 的偏角到达竖直位置时,速度恰好等于0.
的偏角到达竖直位置时,速度恰好等于0.
(1)求电场强度E;
(2)要小球恰好完成竖直圆周运动,求E点释放小球时应有初速度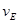 (可含根式)。
(可含根式)。