如图1所示，在某星球表面轻绳约束下的质量为m的小球在竖直平面内做圆周运动，小球在最低点与最高点所受轻绳的拉力之差为ΔF，假设星球是均匀球体，其半径为R，已知万有引力常量为G，不计一切阻力。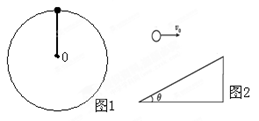
（1）求星球表面重力加速度
（2）求该星球的密度
（3）如图所示2，在该星球表面上，某小球以大小为v0的初速度平抛，恰好能击中倾角为θ的斜面，且位移最短，试求该小球平抛的时间
如图所示，物体A放在足够长的木板B上，木板B静止于水平面。t=0时，电动机通过水平细绳以恒力F拉木板B，使它做初速度为零，加速度aB=1.0m/s2的匀加速直线运动。已知A的质量mA和B的质量mB均为2.0kg,A、B之间的动摩擦因数μ1=0.05，B与水平面之间的动摩擦因数μ2=0.1，最大静摩擦力与滑动摩擦力大小视为相等，重力加速度g取10m/s2。求
（1）物体A刚运动时的加速度aA
（2）t1=1.0s时，电动机的输出功率P；
（3）若t1=1.0s时，将电动机的输出功率立即调整为P1=5W，并在以后的运动过程中始终保持这一功率不变，t2=3.8s时物体A的速度为1.2m/s。则在t1=1.0s到t2=3.8s这段时间内木板B的位移为多少？
如图所示，A、B质量分别为mA=1kg，mB=2kg，AB间用弹簧连接着，弹簧弹性系数k=100N/m，轻绳一端系在A上，另一端跨过定滑轮，B为套在轻绳上的光滑圆环，另一圆环C固定在桌边，B被C挡住而静止在C上，若开始时作用在绳子另一端的拉力F为零，此时A处于静止且刚没接触地面。现用恒定拉力F=15N拉绳子，恰能使B离开C但不能继续上升，不计摩擦且弹簧没超过弹性限度，求
（1）B刚要离开C时A的加速度, （2）若把拉力F改为F=30N，则B刚要离开C时，A的速度。
如图所示，AC为光滑竖直杆，ABC为构成直角的光滑L形轨道，B处有一小圆弧连接可使小球顺利转弯，并且A、B、C三点正好是圆上三点，而AC正好是该圆的直径，如果套在杆上的小球
自A点静止释放(图中小球未画出)，分别沿ABC曲轨道和AC直轨道运动到C点，如果沿ABC曲轨道运动的时间是沿AC直轨道运动所用时间的1.5倍，求AC与AB夹角α的值
如图所示，光滑水平面上静止放置质量M = 2kg，长L = 0.84m的长木板C，离板左端S = 0.12m处静止放置质量mA =1kg的小物块A，A与C间的动摩擦因数μ = 0.4；在板右端静止放置质量mB = 1kg的小物块B，B与C间的摩擦忽略不计．设最大静摩擦力等于滑动摩擦力，A、B均可视为质点，g = 10m/s2．现在木板上加一水平向右的力F，问：
（1）当F = 9N时，小物块A的加速度为多大？
（2）若F足够大，则A与B碰撞之前运动的最短时间是多少？
（3）若在A与B发生碰撞瞬间两者速度交换且此时撤去力F，A最终能滑出C，则F的最大值为多少？
如图所示，将倾角θ=30°、表面粗糙的斜面固定在地面上，用一根轻质细绳跨过两个光滑的半径很小的滑轮连接甲、乙两物体（均可视为质点），把甲物体放在斜面上且细绳与斜面平行，把乙物体悬在空中，并使细绳拉直且偏离竖直方向α=60°。开始时甲、乙均静止。现同时释放甲、乙两物体，乙物体将在竖直平面内往返运动，测得绳长OA为
="0.5" m，当乙物体运动经过最高点和最低点时，甲物体在斜面上均恰好未滑动, 已知乙物体在竖直平面内运动到最低点时的速度大小为
，乙物体的质量为 m="1" kg，忽略空气阻力，取重力加速度g="10" m/s2，求：
（1）乙物体在竖直平面内运动到最低点时所受的拉力大小
（2）甲物体的质量以及斜面对甲物体的最大静摩擦力的大小
（3）斜面与甲物体之间的动摩擦因数μ（设最大静摩擦力等于滑动摩擦力）
粤公网安备 44130202000953号