如图所示，在竖直平面内有一半径为R的半圆轨道与一斜面轨道平滑连接，A、B连线竖直．一质量为m的小球自P点由静止开始下滑，小球沿轨道运动到最高点B时对轨道的压力大小为mg．已知P点与轨道最高点B的高度差为2R，求小球从P点运动到B点的过程中克服摩擦力做了多少功？
如图，在柱形容器中密闭有一定质量气体，一具有质量的光滑导热活塞将容器分为A、B两部分，离气缸底部高为49cm处开有一小孔，与U形水银管相连，容器顶端有一阀门K．先将阀门打开与大气相通，外界大气压等于p0=75cmHg，室温t0=27°C，稳定后U形管两边水银面的高度差为△h=25cm，此时活塞离容器底部为L=50cm．闭合阀门，使容器内温度降至﹣57°C，发现U形管左管水银面比右管水银面高25cm．求：
（1）此时活塞离容器底部高度L′；
（2）整个柱形容器的高度H．
如图所示，是一摩托车特技表演的轨道示意图。AB是距地面高为H的平台上的水平加速轨道，其长度为L，CD是半径为R的
竖直光滑圆弧轨道，CD轨道在最低点D与水平面相切，D点恰好又是紧接的竖直光滑圆形轨道的入口，该圆形轨道的出口与右侧水平减速轨道EF光滑相接。假设某总质量为m的摩托车（可视为质点）由A点从静止开始沿AB轨道做匀加速直线运动，到达B端时关闭发动机后水平飞出，刚好从C点沿切线方向进入圆弧轨道，运动过程中恰能通过圆形轨道的最高点P，最后从E点进入减速轨道直到停止。已知重力加速度为g，不计空气阻力。试求：
（1）摩托车在AB轨道上的加速度a；
（2）竖直圆形轨道的半径；
如图所示，在水平向右的匀强电场中，用长为L的绝缘丝线悬挂一质量为m的带电小球。当小球静止于A点时，丝线与竖直方向成（=30º角。已知电场强度大小为E，重力加速度为g。
（1）试判断小球的带电性质；
（2）求小球所带的电荷量q；
（3）若将小球从丝线与竖直方向成
=60º角的P处（丝线拉直）静止释放，求小球经过悬点O的正下方的最低点时丝线对小球的拉力大小。
如图所示，弹簧AB原长为35cm，A端挂一个重50N的物体，手执B端，将物体置于倾角为30°的斜面上．当物体沿斜面匀速下滑时，弹簧长度为40cm；当物体匀速上滑时，弹簧长度为50cm，试求：
（1）弹簧的劲度系数k；
（2）物体与斜面的动摩擦因数μ
如图甲、乙所示，传送带上有质量均为m的三个木块1、2、3，中间均用原长为L、劲度系数为k的轻弹簧连接起来，木块与传送带间的动摩擦因数均为
，其中木块1被与传送带平行的细线拉住，传送带按图示方向匀速运动，三个木块处于平衡状态．求：
（1）在图甲状态下，1、3两木块之间的距离是多大？
（2）在图乙状态下，细线的拉力是多大？木块1、3之间的距离又是多大？
如图所示，在竖直平面的xoy坐标系内，一根长为l的不可伸长的细绳，一端固定在拉力传感器A上，另一端系一质量为m的小球．x轴上的P点固定一个表面光滑的小钉，P点与传感器A相距
．现拉小球使细绳绷直并处在水平位置，然后由静止释放小球，当细绳碰到钉子后，小球可以绕钉子在竖直平面内做圆周运动．已知重力加速度大小为g，求：
（1）若小球经过最低点时拉力传感器的示数为7mg，求此时小球的速度大小；
（2）传感器A与坐标原点O之间的距离；
（3）若小球经过最低点时绳子恰好断开，请确定小球经过y轴的位置．
如图所示，在一根不可伸长的细线上系一个质量为m的小球，当把小球拉到使细线与水平面成θ=30°角时，轻轻释放小球．不计空气阻力，求小球刚开始做圆周运动的瞬间对细线的拉力．
如图所示，质量为m=
kg的小球置于倾角为30°的光滑固定斜面上，劲度系数为k=200N/m的轻弹簧一端系在小球上，另一端固定在P点，小球静止时，弹簧与竖直方向的夹角为30°．取g=10m/s2．求：
⑴小球对斜面的压力的大小；
⑵弹簧的伸长量；
⑶弹簧被剪断的瞬间，小球的加速度．
如下图所示，质量为3kg的长木板B放在光滑的水平面上，右端与半径R=1m的粗糙的
圆弧相切，左端上方放一质量为1kg物块C，物块C与长木板B间的动摩擦因数
为0.2．现将一质量为1kg的物体A从距圆弧上端h=5m处静止释放，沿着圆弧到达水平
轨道与B碰撞后粘在一起运动，再经1s物块C刚好运动到B
的右端且不会掉下．取g=10m/s．求：
（1）物体A刚进入圆弧时对轨道的压力；
（2）长木板B的长度；
（3）物体A经过圆弧时克服阻力所做的功．
如图所示，弹簧AB原长为25cm，A端挂一个重50N的物体，手执B端，将物体置于倾角为30°的斜面上。当物体沿斜面匀速下滑时，弹簧长度为45cm；当物体匀速上滑时，弹簧长度为55cm，试求：
（1）弹簧的劲度系数；
（2）物体受到的滑动摩擦力的大小。
质量为m＝0.8 kg的砝码悬挂在轻绳PA和PB的结点上并处于静止状态．PA与竖直方向的夹角37°，PB沿水平方向．质量为M＝10kg的木块与PB相连，静止于倾角为37°的斜面上，如图所示．（取g=10m/s2，sin37°=0.6，cos37°=0.8）求：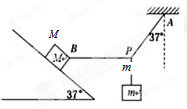
（1）轻绳PB拉力的大小；
（2）木块所受斜面的摩擦力和弹力大小.
游客对过山车的兴趣在于感受到力的变化，这既能让游客感到刺激，但又不会受伤，设计者通过计算“受力因子”来衡量作用于游客身上的力，“受力因子”等于座椅施加给游客的力除以游客自身的重力，可以利用传感器直接显示数值。如图所示为过山车简化原理图：左边部分是装有弹射系统的弹射区，中间部分是作为娱乐主体的回旋区，右边部分是轨道的末端的制动区。某位质量m=60kg游客坐过山车运动过程中，在轨道A处时“受力因子”显示为7，在轨道B处时“受力因子”显示为0.5，在轨道C处时的“受力因子”显示为0.6。己知大回环轨道半径R=10m，重力加速度g取l0m/s2，则
(1)该游客在C处时是超重状态还是失重状态？
(2)求该游客从A处运动到B处过程中损失的机械能；
(3)在设计时能否将弹射区和制动区的位置互换？试用文字定性分析说明。
如图所示，在场强为E的匀强电场中，一绝缘轻质细杆L可绕O点在竖直平面内自由转动，A端有一个带正电的小球，电荷量为q，质量为m。将细杆从水平位置自由释放，则：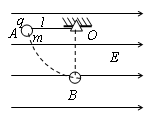
（1）请说明小球由A到B的过程中电势能如何变化?
（2）求出小球在最低点时的速率
（3）求在最低点时绝缘杆对小球的作用力.
），滑块A与水平地面间的最大静摩擦力为正压力的μ倍．问：
粤公网安备 44130202000953号