设 是复数, 表示满足 的最小正整数 ,则对虚数单位 , ( )
| A. |
8 |
B. |
6 |
C. |
4 |
D. |
2 |
已知全集 ,集合 和 的关系的韦恩(Venn)图如下图所示,则阴影部分所示的集合的元素共有( )

| A. |
3个 |
B. |
2个 |
| C. |
1个 |
D. |
无穷个 |
已知抛物线 上一点 到其焦点的距离为 .
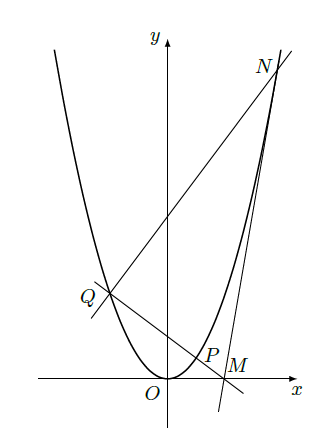
(Ⅰ)求 p于 m的值;
(Ⅱ)设抛物线C上一点 p的横坐标为 t( t>0),过 p的直线交C于另一点 Q,交 x轴于 M点,过点 Q作 PQ的垂线交 C于另一点 N.若 MN是 C的切线,求 t的最小值;
已知函数 .
(Ⅰ)若函数 的图像过原点,且在原点处的切线斜率是-3,求a,b的值;
(Ⅱ)若函数
在区间
上不单调,求a的取值范围. 

设 为数列 的前 n项和, ,其中 是常数.
(Ⅰ)求 及 ;
(Ⅱ)若对于任意的 , , , 成等比数列,求 k的值.
如图, , , , ,P,Q分别为AE,AB的中点.

(Ⅰ)证明: ;
(Ⅱ)求 与 所成角的正弦值.
在 中,角A,B,C所对的边分别为a,b,c,且满足 , .
(Ⅰ)求 的面积;
(Ⅱ)若 ,求 的值.
有20张卡片,每张卡片上分别标有两个连续的自然数k,k+1,其中k=0,1,2,…,19.从这20张卡片中任取一张,记事件"该卡片上两个数的各位数字之和(例如:若取到标有9,10的卡片,则卡片上两个数的各位数字之和为9+1+0=10)不小于14"为A,则P(A)= .
设等差数列 的前n项和为 ,则 , , , 成等差数列.类比以上结论有:设等比数列 的前n项积为 ,则 , , 成等比数列。
某地区居民生活用电分为高峰和低谷两个时间段进行分时计价,该地区的电网销售电价表如下:

若某家庭5月份的高峰时间段用电量为 千瓦时,低谷时间用电量为 千瓦时,则按这种计费方式该家庭本月应付的电费为 元(用数字作答)。