高中数学解答题

已知二次函数经过坐标原点，当 时有最小值，数列的前项和为，点均在函数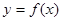的图象上。
（1）求函数的解析式；      
（2）求数列的通项公式；
（3）设是数列的前项和，求使得对所有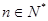都成立的最小正整数．

（本小题满分13分）已知数列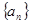的前项和，，等差数列中
（1）求数列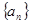、的通项公式；
（2）是否存在正整数，使得 若存在，求出的最小值，若不存在，请说明理由．

已知椭圆的中心在原点，焦点在轴上，离心率为，右焦点到右顶点的距离为．
（1）求椭圆的标准方程；
（2）是否存在与椭圆交于两点的直线：，使得成立？若存在，求出实数的取值范围，若不存在，请说明理由．

（本小题满分10分）选修4-4：坐标系与参数方程
在直角坐标系xOy中，曲线M的参数方程为为参数），若以直角坐标系中的原点O为极点，x轴的正半轴为极轴建立极坐标系，曲线N的极坐标方程为（t为参数）．
（Ⅰ）求曲线M和N的直角坐标方程，
（Ⅱ）若曲线N与曲线M有公共点，求t的取值范围．

（本小题满分12分）已知函数，，其中均为实数．
（Ⅰ）求函数的极值；
（Ⅱ）设，，若对任意的、，恒成立，求实数的最小值；

已知数列的前n项和是，且
（1）证明：为等比数列；
（2）证明：
（3）为数列的前n项和，设，是否存在正整数m，k，使成立，若存在，求出m，k；若不存在，说明理由．

已知函数．
（Ⅰ）求的单调递减区间；
（Ⅱ）若对于任意，都有成立，求实数的取值范围．

（本小题15分）已知△ABC三个顶点的坐标分别是A（0，2），B（1，1），C（1，3）．若△ABC在一个切变变换T作用下变为△A₁B₁C₁，其中B（1，1）在变换T作用下变为点B₁（1，-1）．
（1）求切变变换T所对应的矩阵M；
（2）将△A₁B₁C₁绕原点按顺时针方向旋转45°后得到△A₂B₂C₂．求B₁变化后的对应点B₂的坐标．

如图，已知抛物线的顶点D的坐标为（1，），且与x轴交于A、B两点，与y轴交于C点，A点的坐标为（4，0）．P点是抛物线上的一个动点，且横坐标为m．

（l）求抛物线所对应的二次函数的表达式；
（2）若动点P满足∠PAO不大于45°，求P点的横坐标m的取值范围；
（3）当P点的横坐标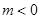时，过p点作y轴的垂线PQ，垂足为Q．问：是否存在P点，使∠QPO=∠BCO？若存在，请求出P点的坐标；若不存在，请说明理由．

阅读理解材料一：一组对边平行，另一组对边不平行的四边形叫梯形，其中平行的两边叫梯形的底边，不平行的两边叫梯形的腰，连接梯形两腰中点的线段叫梯形的中位线．梯形的中位线具有以下性质：梯形的中位线平行于两底，并且等于两底和的一半．
如图（1）：在梯形ABCD中：AD∥BC，
∵E、F是AB、CD的中点，∴EF∥AD∥BC，EF=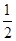（AD+BC）

材料二：经过三角形一边的中点与另一边平行的直线必平分第三边
如图（2）：在△ABC中：∵E是AB的中点，EF∥BC
∴F是AC的中点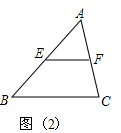

请你运用所学知识，结合上述材料，解答下列问题．
如图（3）在梯形ABCD中，AD∥BC，AC⊥BD于O，E、F分别为AB、CD的中点，∠DBC=30°．

（1）求证：EF=AC；
（2）若OD=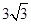，OC=5，求MN的长．

如图，是坐标原点，过点的抛物线与轴的另一个交点为，与轴交于点，其顶点为点．

（1）求的值．
（2）连结、，动点的坐标为．
①当四边形是平行四边形时，求的值；
②连结、，当最大时，求出点的坐标．

已知：如图，点A（3，4）在直线y=kx上，过A作AB⊥x轴于点B．

（1）求k的值；
（2）设点B关于直线y=kx的对称点为C点，求ΔABC外接圆的面积；
（3）抛物线y=－1与x轴的交点为Q，试问在直线y=kx上是否存在点P，使得
∠CPQ=∠OAB，如果存在，请求出P点的坐标；如果不存在，请说明理由．

如图，在平面直角坐标系中，矩形OCDE的三个顶点分别是C（3，0），D（3，4），E（0，4）．点A在DE上，以A为顶点的抛物线过点C，且对称轴x=1交x轴于点B．连接EC，AC．点P，Q为动点，设运动时间为t秒．

（1）填空：点A坐标为  ；抛物线的解析式为             ．
（2）在图1中，若点P在线段OC上从点O向点C以1个单位/秒的速度运动，同时，点Q在线段CE上从点C向点E以2个单位/秒的速度运动，当一个点到达终点时，另一个点随之停止运动．当t为何值时，△PCQ为直角三角形？
（3）在图2中，若点P在对称轴上从点A开始向点B以1个单位/秒的速度运动，过点P做PF⊥AB，交AC于点F，过点F作FG⊥AD于点G，交抛物线于点Q，连接AQ，CQ．当t为何值时，△ACQ的面积最大？最大值是多少？

如图，在矩形OABC中，AO=10，AB=8，沿直线CD折叠矩形OABC的一边BC，使点B落在OA边上的点E处．分别以OC，OA所在的直线为x轴，y轴建立平面直角坐标系，抛物线y=ax²+bx+c经过O，D，C三点．

（1）求AD的长及抛物线的解析式；
（2）一动点P从点E出发，沿EC以每秒2个单位长的速度向点C运动，同时动点Q从点C出发，沿CO以每秒1个单位长的速度向点O运动，当点P运动到点C时，两点同时停止运动．设运动时间为t秒，当t为何值时，以P、Q、C为顶点的三角形与△ADE相似？
（3）点N在抛物线对称轴上，点M在抛物线上，是否存在这样的点M与点N，使以M，N，C，E为顶点的四边形是平行四边形？若存在，请直接写出点M与点N的坐标（不写求解过程）；若不存在，请说明理由．

【问题探究】
（1）如图1，锐角△ABC中，分别以AB、AC为边向外作等腰△ABE和等腰△ACD，使AE=AB，AD=AC，∠BAE=∠CAD，连接BD，CE，试猜想BD与CE的大小关系，并说明理由．
【深入探究】
（2）如图2，四边形ABCD中，AB=7cm，BC=3cm，∠ABC=∠ACD=∠ADC=45º，求BD的长．
（3）如图3，在（2）的条件下，当△ACD在线段AC的左侧时，求BD的长．