(本小题满分12分)
已知椭圆C的中心在原点、焦点在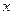 轴上,椭圆C上的点到焦点的最大值为3,最小值为1.
轴上,椭圆C上的点到焦点的最大值为3,最小值为1.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若直线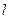 :
: 与
与 椭圆交于不同的两点M,N(M,N不是左、右顶点),且以MN为直径的圆经过椭圆的右顶点A.求证:直线
椭圆交于不同的两点M,N(M,N不是左、右顶点),且以MN为直径的圆经过椭圆的右顶点A.求证:直线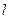 过定点,并求出定点的坐标.
过定点,并求出定点的坐标.
(本小题满分12分)
已知数列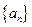 中,
中,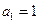 ,且点
,且点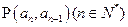 在直线
在直线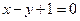 上. (Ⅰ)求数列
上. (Ⅰ)求数列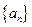 的通项公式;(Ⅱ)若函数
的通项公式;(Ⅱ)若函数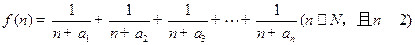 ,求函数
,求函数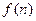 的最小值; (Ⅲ)设
的最小值; (Ⅲ)设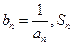 表示数列
表示数列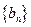 的前
的前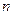 项和.试问:是否存在关于
项和.试问:是否存在关于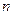 的整式
的整式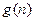 ,使得
,使得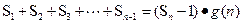 对于一切不小于2的自然数
对于一切不小于2的自然数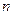 恒成立?若存在,写出
恒成立?若存在,写出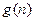 的解析式,并加以证明;若不存在,试说明理由.
的解析式,并加以证明;若不存在,试说明理由.
(本小题满分12分)
为应对国际金融危机对企业带来的不良影响,2009年某企业实行裁员增效,已知现有员工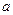 人,每人每年可创纯利润1万元.据评估,在生产条件不变的条件下,每裁员一人,则留岗员工每人每年可多创收0.01万元,但每年需付给下岗工人0.4万元生活费,并且企业正常运行所需人数不得少于现有员工的
人,每人每年可创纯利润1万元.据评估,在生产条件不变的条件下,每裁员一人,则留岗员工每人每年可多创收0.01万元,但每年需付给下岗工人0.4万元生活费,并且企业正常运行所需人数不得少于现有员工的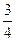 ,设该企业裁员
,设该企业裁员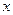 人后纯收益为
人后纯收益为 万元.
万元.
(Ⅰ)写出 关于
关于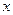 的函数关系式,并指出
的函数关系式,并指出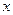 的取值范围;
的取值范围;
(Ⅱ)当140<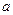 ≤280时,问企业裁员多少人,才能获得最大的经济效益?(注:在保证能获得最大经济效益的情况下,能少裁员,应尽量少裁)
≤280时,问企业裁员多少人,才能获得最大的经济效益?(注:在保证能获得最大经济效益的情况下,能少裁员,应尽量少裁)
(本小题满分12分)
如图,在直三棱柱 中,AB=1,AC=2,
中,AB=1,AC=2, ,D,E分别是
,D,E分别是 和
和 的中点.
的中点.
(Ⅰ)证明:DE∥平面ABC;
(Ⅱ)求直线DE与平面 所成的角.
所成的角.
(本小题满分12分) 设甲、乙两套试验方案在一次试验中成功的概率均为 ,且这两套试验方案中至少有一套试验成功的概率为0.51,假设这两套试验方案在试验过程中,相互之间没有影响.设试验成功的方案的个数
,且这两套试验方案中至少有一套试验成功的概率为0.51,假设这两套试验方案在试验过程中,相互之间没有影响.设试验成功的方案的个数 . (Ⅰ)求
. (Ⅰ)求 的值; (Ⅱ)求
的值; (Ⅱ)求 的数学期望
的数学期望 与方差
与方差 .
.
(本小题满分10分)
已知A,B,C是 的内角,
的内角, 分别是其对边长,
分别是其对边长,
向量 .
.
(Ⅰ)求角A的大小; (Ⅱ)若 ,求
,求 的长.
的长.
(本小题满分12分)
已知椭圆C的中心在原点、焦点在 轴上,椭圆C上的点到焦点的最大值为3,最小值为1.
轴上,椭圆C上的点到焦点的最大值为3,最小值为1.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若直线 :
: 与
与 椭圆交于不同的两点M,N(M,N不是左、右顶点),且以MN为直径的圆经过椭圆的右顶点A.求证:直线
椭圆交于不同的两点M,N(M,N不是左、右顶点),且以MN为直径的圆经过椭圆的右顶点A.求证:直线 过定点,并求出定点的坐标.
过定点,并求出定点的坐标.
(本小题满分12分)
已知数列 中,
中, ,且点
,且点 在直线
在直线 上. (Ⅰ)求数列
上. (Ⅰ)求数列 的通项公式;(Ⅱ)若函数
的通项公式;(Ⅱ)若函数 ,求函数
,求函数 的最小值; (Ⅲ)设
的最小值; (Ⅲ)设 表示数列
表示数列 的前
的前 项和.试问:是否存在关于
项和.试问:是否存在关于 的整式
的整式 ,使得
,使得 对于一切不小于2的自然数
对于一切不小于2的自然数 恒成立?若存在,写出
恒成立?若存在,写出 的解析式,并加以证明;若不存在,试说明理由.
的解析式,并加以证明;若不存在,试说明理由.
(本小题满分12分)
为应对国际金融危机对企业带来的不良影响,2009年某企业实行裁员增效,已知现有员工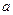 人,每人每年可创纯利润1万元.据评估,在生产条件不变的条件下,每裁员一人,则留岗员工每人每年可多创收0.01万元,但每年需付给下岗工人0.4万元生活费,并且企业正常运行所需人数不得少于现有员工的
人,每人每年可创纯利润1万元.据评估,在生产条件不变的条件下,每裁员一人,则留岗员工每人每年可多创收0.01万元,但每年需付给下岗工人0.4万元生活费,并且企业正常运行所需人数不得少于现有员工的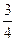 ,设该企业裁员
,设该企业裁员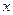 人后纯收益为
人后纯收益为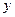 万元.
万元.
(Ⅰ)写出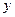 关于
关于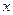 的函数关系式,并指出
的函数关系式,并指出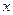 的取值范围;
的取值范围;
(Ⅱ)当140<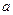 ≤280时,问企业裁员多少人,才能获得最大的经济效益?(注:在保证能获得最大经济效益的情况下,能少裁员,应尽量少裁)
≤280时,问企业裁员多少人,才能获得最大的经济效益?(注:在保证能获得最大经济效益的情况下,能少裁员,应尽量少裁)
(本小题满分12分)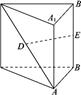
如图,在直三棱柱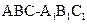 中,AB=1,AC=2,
中,AB=1,AC=2,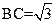 ,D,E分别是
,D,E分别是 和
和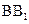 的中点.
的中点.
(Ⅰ)证明:DE∥平面ABC;
(Ⅱ)求直线DE与平面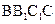 所成的角.
所成的角.
(本小题满分10分)
已知A,B,C是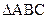 的内角,
的内角,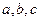 分别是其对边长,
分别是其对边长,
向量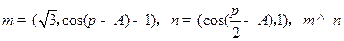 .
.
(Ⅰ)求角A的大小; (Ⅱ)若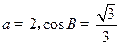 ,求
,求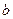 的长.
的长.
(本小题满分12分)
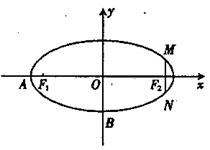
如图,在直角坐标系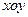 中,已知椭圆
中,已知椭圆 :
: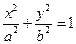
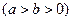 的离心率
的离心率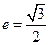 ,左、右两个焦点分别为
,左、右两个焦点分别为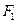 、
、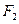 。过右焦点
。过右焦点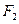 且与
且与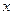 轴垂直的直线与椭圆
轴垂直的直线与椭圆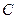 相交
相交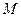 、
、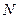 两点,且
两点,且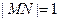 .
.
(1)求椭圆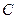 的方程;
的方程;
(2)设椭圆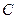 的左顶点为
的左顶点为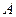 ,下顶点为
,下顶点为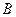 ,动点
,动点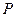 满足
满足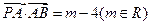 ,试求点
,试求点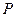 的轨迹方程,使点
的轨迹方程,使点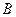 关于该轨迹的对称点落在椭圆
关于该轨迹的对称点落在椭圆 上.
上.