(本小题14分)设函数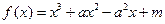
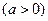
(1)若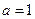 时函数
时函数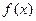 有三个互不相同的零点,求
有三个互不相同的零点,求 的范围;
的范围;
(2)若函数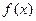 在
在 内没有极值点,求
内没有极值点,求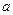 的范围;
的范围;
(3)若对任意的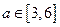 ,不等式
,不等式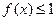 在
在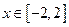 上恒成立,求实数
上恒成立,求实数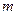 的取值范围.
的取值范围.
(本小题13分)已知定点 及椭圆
及椭圆 ,过点
,过点 的动直线与该椭圆相交于
的动直线与该椭圆相交于 两点.
两点.
(1)若线段 中点的横坐标是
中点的横坐标是 ,求直线
,求直线 的方程;
的方程;
(2)在 轴上是否存在点
轴上是否存在点 ,使
,使 为常数?若存在,求出点
为常数?若存在,求出点 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
(本小题12分)已知数列 的前
的前 项和
项和 (
( 为正整数)
为正整数)
(1)求数列 的通项公式;
的通项公式;
(2)若 ,
, ,求
,求 .
.
(本小题12分)如图,四棱椎 的底面为菱形,且
的底面为菱形,且 ,
, 平面
平面 ,
, ,
, 为
为 的中点.
的中点.
(1)求直线 与平面
与平面 所成角的正切值;
所成角的正切值;
(2)在线段 上是否存在一点
上是否存在一点 ,使
,使 面
面 成立?如果存在,求出
成立?如果存在,求出 的长;如果不存在,请说明理由.
的长;如果不存在,请说明理由.
(本小题12分)某校设计了一个实验学科的实验考察方案:考生从6道备选题中一次性随机抽取3题,按照题目要求独立完成全部实验操作。规定:至少正确完成其中2题的便可通过考察,已知6道备选题中考生甲有4题能正确完成,2题不能完成;考生乙每题正确完成的概率都是 ,且每题正确完成与否互不影响。求:
,且每题正确完成与否互不影响。求:
(1)分别写出甲、乙两个考生正确分析完成题数的概率分布列;
(2)分析哪个考生通过考察的概率较大?
(本小题12分)已知 是
是 的三个内角,向量
的三个内角,向量
 ,且
,且 .
.
(1)求角 ;
;
(2)若
 ,求
,求 .
.
(本小题满分7分)选修4-4:坐标系与参数方程
已知极坐标系的极点在直角坐标系的原点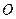 处,极轴与
处,极轴与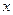 轴的正半轴重合.直线l的极坐标方程为
轴的正半轴重合.直线l的极坐标方程为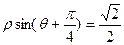 ,圆
,圆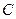 的参数方程为
的参数方程为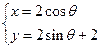 (参数
(参数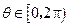 ),求圆心
),求圆心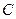 到直线
到直线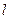 的距离.
的距离.
(本小题满分7分)选修4-2:矩阵与变换
已知矩阵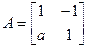 ,其中
,其中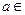 R,若点P(1,1)在矩阵A的变换下得到点P′(0,-3),求矩阵A的特征值及特征向量.
R,若点P(1,1)在矩阵A的变换下得到点P′(0,-3),求矩阵A的特征值及特征向量.
已知函数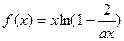 的定义域为
的定义域为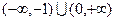 .
.
(Ⅰ)求实数 的值;(Ⅱ)探究
的值;(Ⅱ)探究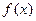 是否是
是否是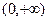 上的单调函数?若是,请证明;若不是,请说明理由; (Ⅲ)求证:
上的单调函数?若是,请证明;若不是,请说明理由; (Ⅲ)求证: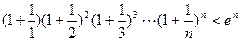 ,
,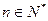 (其中
(其中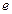 为自然对数的底数).
为自然对数的底数).
已知抛物线C的方程为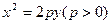 ,A,B是抛物线C上的两点,直线AB过点M
,A,B是抛物线C上的两点,直线AB过点M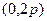 。(Ⅰ)设
。(Ⅰ)设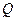 是抛物线上任意一点,求
是抛物线上任意一点,求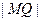 的最小值; (Ⅱ)求向量
的最小值; (Ⅱ)求向量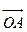 与向量
与向量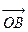 的夹角(O是坐标原点);(Ⅲ)在
的夹角(O是坐标原点);(Ⅲ)在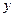 轴上是否存在异于M的一点N,直线AN与抛物线的另一个交点为D,而直线DB与
轴上是否存在异于M的一点N,直线AN与抛物线的另一个交点为D,而直线DB与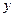 轴交于点E,且有
轴交于点E,且有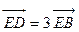 ?若存在,求出N点坐标;若不存在,说明理由.
?若存在,求出N点坐标;若不存在,说明理由.
(本小题满分13分)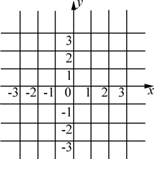 设不等式组
设不等式组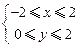 确定的平面区域为U,
确定的平面区域为U,
确定的平面区域为V.(Ⅰ)定义坐标为整数的点为“整点”.
在区域U内任取3个整点,
求这些整点中恰有2个整点在区域V的概率;
(Ⅱ)在区域U内任取3个点,记此3个点在区域V的个数为X,
求X的概率分布列及其数学期望.
设函数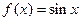 ,
,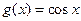 ,(Ⅰ)如果函数
,(Ⅰ)如果函数 的图像是由函数
的图像是由函数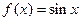 的图像上各点的横坐标伸长为原来的2倍,再把所得图像向左平移
的图像上各点的横坐标伸长为原来的2倍,再把所得图像向左平移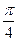 得到,求函数
得到,求函数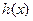 解析式;
解析式;
(Ⅱ)如果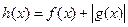 ,求
,求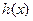 在区间
在区间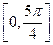 上的值域.
上的值域.