福建省南平市高中毕业班适应性考试数学试题(理科)
为了解某校高三学生的视力情况,随机地
抽查了该校100名高三学生的视力情况,
得到频率分布直方图,如右,由于不慎将
部分数据丢失,但知道前4组的频数成等
比数列,后6组的频数成等差数列,设最
大频率为a,视力在4.6到5.0之间的
学生数为b,则a, b的值分别为( )
| A.0.27, 78 | B.0.27, 83 |
| C.2.7, 78 | D.2.7, 83 |
 |
(本小题满分13分) 设不等式组
设不等式组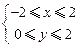 确定的平面区域为U,
确定的平面区域为U,
确定的平面区域为V.(Ⅰ)定义坐标为整数的点为“整点”.
在区域U内任取3个整点,
求这些整点中恰有2个整点在区域V的概率;
(Ⅱ)在区域U内任取3个点,记此3个点在区域V的个数为X,
求X的概率分布列及其数学期望.
已知抛物线C的方程为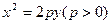 ,A,B是抛物线C上的两点,直线AB过点M
,A,B是抛物线C上的两点,直线AB过点M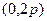 。(Ⅰ)设
。(Ⅰ)设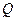 是抛物线上任意一点,求
是抛物线上任意一点,求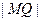 的最小值; (Ⅱ)求向量
的最小值; (Ⅱ)求向量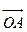 与向量
与向量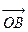 的夹角(O是坐标原点);(Ⅲ)在
的夹角(O是坐标原点);(Ⅲ)在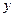 轴上是否存在异于M的一点N,直线AN与抛物线的另一个交点为D,而直线DB与
轴上是否存在异于M的一点N,直线AN与抛物线的另一个交点为D,而直线DB与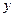 轴交于点E,且有
轴交于点E,且有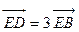 ?若存在,求出N点坐标;若不存在,说明理由.
?若存在,求出N点坐标;若不存在,说明理由.
(本小题满分7分)选修4-4:坐标系与参数方程
已知极坐标系的极点在直角坐标系的原点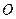 处,极轴与
处,极轴与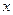 轴的正半轴重合.直线l的极坐标方程为
轴的正半轴重合.直线l的极坐标方程为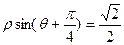 ,圆
,圆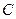 的参数方程为
的参数方程为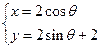 (参数
(参数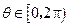 ),求圆心
),求圆心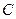 到直线
到直线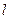 的距离.
的距离.
 ,则
,则 ( )
( )
 ”的否定是 ( )
”的否定是 ( )

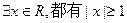

 2a14的值为 ( )
2a14的值为 ( ) ,AC=2,
,AC=2, ,则
,则 = ( )
= ( )



 执行如图所示的程序框图,若输出的b的值为16,
执行如图所示的程序框图,若输出的b的值为16, 上是减函数,则
上是减函数,则 的取值范围是 ( )
的取值范围是 ( )



 积等于 ( )
积等于 ( )



 外心,
外心,  ,则
,则 ( )
( )


 、
、 ,定义
,定义 ,
, .设
.设 ,
, ,则
,则 为 ( )
为 ( )



 关于直线
关于直线 对称的直线方程是 .
对称的直线方程是 . 展开式的各项系数之和为32,则展开式中的常数项为 .(用数字作答)
展开式的各项系数之和为32,则展开式中的常数项为 .(用数字作答) 在区间[
在区间[ 上的最大值与最小值的和 .
上的最大值与最小值的和 . ),(
),( ),(
),( ),(
),( ),…,(
),…,( ),…
),… ),(
),( ),(
),( ),…,则
),…,则 = .
= . ,椭圆C:
,椭圆C: 的右焦点为
的右焦点为 ,直线
,直线 的方程为
的方程为 ,点A在直线
,点A在直线 ,则直线AF的倾斜角的大小为 .
,则直线AF的倾斜角的大小为 .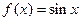 ,
,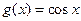 ,(Ⅰ)如果函数
,(Ⅰ)如果函数 的图像是由函数
的图像是由函数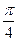 得到,求函数
得到,求函数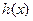 解析式;
解析式;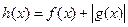 ,求
,求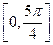 上的值域.
上的值域.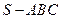 中,侧面
中,侧面 与侧面
与侧面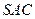 均为等边三角形,
均为等边三角形, ,
,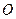 为
为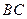 中点.
中点.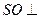 平面
平面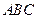 ;
;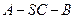 的余弦值.
的余弦值.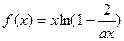 的定义域为
的定义域为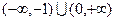 .
. 的值;(Ⅱ)探究
的值;(Ⅱ)探究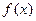 是否是
是否是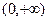 上的单调函数?若是,请证明;若不是,请说明理由; (Ⅲ)求证:
上的单调函数?若是,请证明;若不是,请说明理由; (Ⅲ)求证: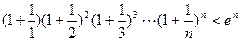 ,
,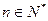 (其中
(其中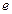 为自然对数的底数).
为自然对数的底数).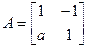 ,其中
,其中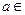 R,若点P(1,1)在矩阵A的变换下得到点P′(0,-3),求矩阵A的特征值及特征向量.
R,若点P(1,1)在矩阵A的变换下得到点P′(0,-3),求矩阵A的特征值及特征向量.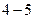 ;不等式选讲
;不等式选讲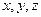 为正实数,且
为正实数,且 ,求
,求 的最小值及取得最小值时
的最小值及取得最小值时 粤公网安备 44130202000953号
粤公网安备 44130202000953号