河南省长葛市模拟试卷二数学试题(理)
已知f (x)为偶函数,且f (2+x)=f (2-x),当-2≤x≤0时,f (x)=2x, an=f (n), n∈N*,则a2010的值为
A.2010 B.4 
 D.-4
D.-4
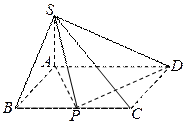 如图,四棱锥
如图,四棱锥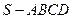 的底面是矩形,
的底面是矩形,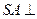 底面
底面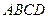 ,P为BC边的中点,SB与
,P为BC边的中点,SB与
平面ABCD所成的角为45°,且AD=2,SA=1.
(1)求证: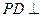 平面SAP;
平面SAP;
(2)求二面角A-SD-P的大小.
某社区举办2010年上海世博会知识宣传活动,进行现场抽奖,抽奖规则是:盒中装有10张大小相同的精美卡片,卡片上分别印有“世博会会徽”或“海宝”(世博会吉祥物)图案,参加者每次从盒中抽取卡片两张,若抽到两张都是“海宝”卡即可获奖.
(1)活动开始后,一位参加者问:盒中有几张“海宝”卡?主持人笑说:我只知道若从盒中抽两张都不是“海宝”卡的概率是 ,求抽奖者获奖的概率;
,求抽奖者获奖的概率;
(2)现有甲乙丙丁四人依次抽奖,抽后放回,另一个人再抽,用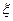 表示获奖的人数,求
表示获奖的人数,求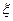 的分布列及
的分布列及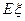 .
.
在数列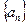 中,已知a1=2,an+1=4an-3n+1,n∈
中,已知a1=2,an+1=4an-3n+1,n∈ .
.
(1)设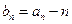 ,求数列
,求数列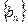 的通项公式;
的通项公式;
(2)设数列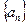 的前n项和为Sn,证明:对任意的n∈
的前n项和为Sn,证明:对任意的n∈ ,不等式Sn+1≤4Sn恒成立.
,不等式Sn+1≤4Sn恒成立.
 ,集合
,集合 ,则“
,则“ ”是“
”是“ ”的
”的 充分必要条件 D.既不充分也不必要条件
充分必要条件 D.既不充分也不必要条件 为虚数单位,且
为虚数单位,且 ,则
,则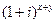 的值为
的值为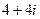 B.
B.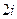
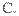 4 D.
4 D.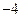
 的值为
的值为 21 D.12
21 D.12 的焦点,且方向向量为
的焦点,且方向向量为 的直线
的直线 的方程是
的方程是 B.
B.

 D.
D.
 中,
中, ,数列
,数列 是等比数列,且
是等比数列,且 ,则b6b8的值为
,则b6b8的值为 B.
B.

 D.
D.
 具有性质
具有性质 ,图象关于直线
,图象关于直线 对称
对称 最大值为
最大值为 对称
对称 112种 D.140种
112种 D.140种 、
、 满足条件
满足条件 ,那么
,那么 的最大值为
的最大值为
 D.
D.
 是函数f(x)=2x-()x+x的反函数,则
是函数f(x)=2x-()x+x的反函数,则 B.
B.

 D.
D.
 、
、 、
、 .则三棱锥A—BCD的外接球的体积为
.则三棱锥A—BCD的外接球的体积为 B.
B.

 D.
D.
 的左、右焦点,A是其右顶点,过F2作
的左、右焦点,A是其右顶点,过F2作 轴的垂线与双曲线的一个交点为P,G是
轴的垂线与双曲线的一个交点为P,G是 ,则双曲线的离心率是
,则双曲线的离心率是
 3 D.
3 D.
 展开式中,常数项是 ★ .
展开式中,常数项是 ★ . 中,三内角
中,三内角 所对边的长分别为
所对边的长分别为 ,已知
,已知 ,不等式
,不等式 的解集为
的解集为 ,则
,则 ★ .
★ . 和圆
和圆 都相切的半径最小的圆的方程是
都相切的半径最小的圆的方程是 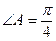 ,设
,设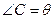 .
.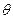 表示b;
表示b;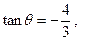 求
求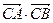 的值.
的值.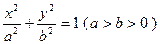 ,它的一个顶点为
,它的一个顶点为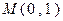 ,离心率
,离心率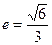 .
.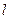 与椭圆交于A,B两点,坐标原点O到直线l的距离为
与椭圆交于A,B两点,坐标原点O到直线l的距离为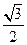 ,求△AOB面积的最大值.
,求△AOB面积的最大值.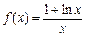 .
.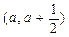 (其中
(其中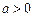 )上存在极值,求实数a的取值范围;
)上存在极值,求实数a的取值范围;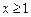 时,不等式
时,不等式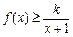 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号