已知函数 ,其中
,其中 .
.
(1)当 时,求曲线
时,求曲线 的点
的点 处的切线方程;
处的切线方程;
(2)当 时,若
时,若 在区间
在区间 上的最小值为-2,求
上的最小值为-2,求 的取值范围;
的取值范围;
(3)若 ,且
,且 恒成立,求
恒成立,求 的取值范围.
的取值范围.
如图,三棱柱 中,
中, 平面
平面 ,
, ,
, , 点
, 点 在线段
在线段 上,且
上,且 ,
, .
.
(Ⅰ)求证:直线 与平面
与平面 不平行;
不平行;
(Ⅱ)设平面 与平面
与平面 所成的锐二面角为
所成的锐二面角为 ,若
,若 ,求
,求 的长;
的长;
(Ⅲ)在(Ⅱ)的条件下,设平面 平面
平面 ,求直线
,求直线 与
与 所成的角的余弦值.
所成的角的余弦值.
已知数列 的前
的前 项和为
项和为 ,且
,且 .
.
(1)求 的通项公式;
的通项公式;
(2)设 ,若
,若 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)设 ,
, 是数列
是数列 的前
的前 项和,证明
项和,证明 .
.
某学校假期后勤维修的一项工作是请30名木工制作200把椅子和100张课桌.已知一名工人在单位时间内可制作10把椅子或7张课桌.将这30名工人分成两组,一组制作课桌,一组制作椅子,两组同时开工.设制作课桌的工人为 名.
名.
(1)分别用含 的式子表示制作200把椅子和100张课桌所需的单位时间;
的式子表示制作200把椅子和100张课桌所需的单位时间;
(2)当 为何值时,完成此项工作的时间最短?
为何值时,完成此项工作的时间最短?
已知函数 .
.
(1)若x=2是函数f(x)的极值点,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若函数f(x)在 上为单调增函数,求a的取值范围;
上为单调增函数,求a的取值范围;
(3)设m,n为正实数,且m>n,求证: .
.
如图所示,AD⊥平面ABC,CE⊥平面ABC,AC=AD=AB=1, ,凸多面体ABCED的体积为
,凸多面体ABCED的体积为 ,F为BC的中点.
,F为BC的中点.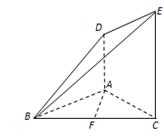
(1)求证:AF∥平面BDE;
(2)求证:平面BDE⊥平面BCE.
某同学用“五点法”画函数 在某一个周期的图象时,列表并填入了部分数据,如下表:
在某一个周期的图象时,列表并填入了部分数据,如下表:
(1)请求出上表中的 ,
, ,
,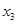 ,并直接写出函数f(x)的解析式;
,并直接写出函数f(x)的解析式;
(2)将f(x)的图象沿x轴向右平移 个单位得到函数g(x),若函数g(x)在
个单位得到函数g(x),若函数g(x)在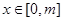 (其中
(其中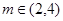 )上的值域为
)上的值域为 ,且此时其图象的最高点和最低点分别为P,Q,求
,且此时其图象的最高点和最低点分别为P,Q,求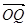 与
与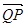 夹角
夹角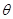 的大小.
的大小.
如图1,在Rt△ABC中,∠C=90°,BC=6,AC=3,D,E分别是AC,AB上的点,且DE∥BC,DE=4,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图2.
(1)求证: 平面
平面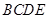 ;
;
(2)过点E作截面
 平面
平面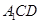 ,分别交CB于F,
,分别交CB于F, 于H,求截面
于H,求截面 的面积。
的面积。
如图,正方体 中,E为AB中点,F为正方形BCC1B1的中心.
中,E为AB中点,F为正方形BCC1B1的中心.
(1)求直线EF与平面ABCD所成角的正切值;
(2)求异面直线A1C与EF所成角的余弦值.