某学校假期后勤维修的一项工作是请30名木工制作200把椅子和100张课桌．已知一名工人在单位时间内可制作10把椅子或7张课桌．将这30名工人分成两组，一组制作课桌，一组制作椅子，两组同时开工．设制作课桌的工人为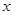
名．
（1）分别用含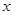的式子表示制作200把椅子和100张课桌所需的单位时间；
（2）当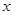为何值时，完成此项工作的时间最短？
相关试题
的焦点分别是
和
，已知椭圆的离心率
过中心
作直线与椭圆交于A，B两点，
的面积是20，
的值（2）直线AB的方程
上，M
垂直于椭圆焦点所在的直线，垂足为
为线段M
的中点，求
表示的平面区域，并求平面区域面积。
的前n项和为
，已知
，
。求
和推荐套卷
某学校假期后勤维修的一项工作是请30名木工制作200把椅子和100张课桌．已知一名工人在单位时间内可制作10把椅子或7张课桌．将这30名工人分成两组，一组制作课桌，一组制作椅子，两组同时开工．设制作课桌的工人为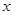名．
（1）分别用含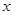的式子表示制作200把椅子和100张课桌所需的单位时间；
（2）当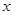为何值时，完成此项工作的时间最短？
粤公网安备 44130202000953号