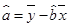已知函数 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当 时,
时, .
.
(Ⅰ)现已画出函数 在y轴左侧的图象,如图所示,请补出完整函数
在y轴左侧的图象,如图所示,请补出完整函数 的图象,并根据图象写出函数
的图象,并根据图象写出函数 的增区间;
的增区间;
(Ⅱ)求出函数 的解析式和值域.
的解析式和值域.
已知函数
(Ⅰ)判断函数的奇偶性,并加以证明;
(Ⅱ)用定义证明 在
在 上是增函数;
上是增函数;
(Ⅲ)求出函数 在
在 的最值.
的最值.
(本小题只理科做,满分14分)如图,已知 平面
平面 ,
, ,△
,△ 是正三角形,
是正三角形, ,且
,且 是
是 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求证:平面 平面
平面 ;
;
(3)求平面 与平面
与平面 所成锐二面角的大小.
所成锐二面角的大小.
(本小题文科14分理科13分).某公司今年初用25万元引进一种新的设备,设备投入运行后,每年销售收入为21万元。已知该公司第n年需要付出设备的维修和工人工资等费用的和 的信息如下图。
的信息如下图。
(1)求 ;
;
(2)该公司引进这种设备后,第几年后开始获利、第几年后开始亏损?
(3)这种设备使用多少年,该公司的年平均获利最大?( )
)
(本小题文科14分,理科12分)已知方程 的曲线是圆C
的曲线是圆C
(1)求 的取值范围;
的取值范围;
(2)当 时,求圆C截直线
时,求圆C截直线
 所得弦长;
所得弦长;
(3) 若圆C与直线 相交于
相交于 两点,且以
两点,且以 为直径的圆过坐标原点O,
为直径的圆过坐标原点O,
求 的值.
的值.
(本小题满分12分)甲,乙两人约定上午7:00至8:00之间到某站乘公共汽车,在这段时间内有2班公共汽车,它们开车的时刻分别是7:30和8:00,甲、乙两人约定,见车就乘,则甲、乙同乘一车的概率为(假定甲、乙两人到达车站的时刻是互相不牵连的,且每人在7时到8时的任何时刻到达车站是等可能的).
(本小题只理科做,满分14分)如图,已知 平面
平面 ,
, ,△
,△ 是正三角形,
是正三角形,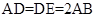 ,且
,且 是
是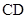 的中点.
的中点.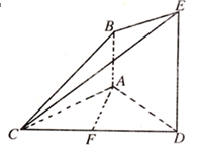
(1)求证: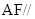 平面
平面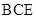 ;
;
(2)求证:平面 平面
平面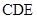 ;
;
(3)求平面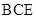 与平面
与平面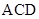 所成锐二面角的大小.
所成锐二面角的大小.
(本小题文科14分理科13分).某公司今年初用25万元引进一种新的设备,设备投入运行后,每年销售收入为21万元。已知该公司第n年需要付出设备的维修和工人工资等费用的和 的信息如下图。
的信息如下图。
(1)求 ;
;
(2)该公司引进这种设备后,第几年后开始获利、第几年后开始亏损?
(3)这种设备使用多少年,该公司的年平均获利最大?( )
)
(本小题文科14分,理科12分)已知方程 的曲线是圆C
的曲线是圆C
(1)求 的取值范围;
的取值范围;
(2)当 时,求圆C截直线
时,求圆C截直线
 所得弦长;
所得弦长;
(3)若圆C与直线 相交于
相交于 两点,且以
两点,且以 为直径的圆过坐标原点O,求
为直径的圆过坐标原点O,求 的值.
的值.
(本小题满分12分)甲,乙两人约定上午7:00至8:00之间到某站乘公共汽车,在这段时间内有2班公共汽车,它们开车的时刻分别是7:30和8:00,甲、乙两人约定,见车就乘,则甲、乙同乘一车的概率为(假定甲、乙两人到达车站的时刻是互相不牵连的,且每人在7时到8时的任何时刻到达车站是等可能的).
(本小题满分12分)某地区2007年至2013年农村居民家庭纯收入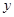 (单位:千元)的数据如下表:
(单位:千元)的数据如下表:
| 年份 |
2007 |
2008 |
2009 |
2010 |
2011 |
2012 |
2013 |
年份代号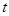 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
人均纯收入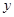 |
2.9 |
3.3 |
3.6 |
4.4 |
4.8 |
5.2 |
5.9 |
(Ⅰ)求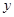 关于
关于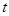 的线性回归方程;(已知b=0.5)
的线性回归方程;(已知b=0.5)
(Ⅱ)利用(Ⅰ)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
(本小题满分12分)以下茎叶图记录了甲、乙两组各三名同学在期末考试中的数学成绩.乙组记录中有一个数字模糊,无法确认,假设这个数字具有随机性,并在图中以 表示.
表示. 
(1)若甲、乙两个小组的数学平均成绩相同,求 的值;
的值;
(2)当 时,分别从甲、乙两组同学中各随机选取一名同学,求这两名同学的数学成绩之差的绝对值不超过2分的概率.
时,分别从甲、乙两组同学中各随机选取一名同学,求这两名同学的数学成绩之差的绝对值不超过2分的概率.
(本小题满分14分)数列 满足:
满足: ;
;
(1)证明:数列 是单调递减数列的充要条件是:
是单调递减数列的充要条件是: ;
;
(2)求 的取值范围,使数列
的取值范围,使数列 是单调递增数列.
是单调递增数列.
(本小题满分12分) 一个黑色小布袋,袋中有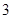 只黄色、
只黄色、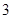 只红色的乒乓球(除颜色外其体积、质地完全相同),从袋中随机摸出
只红色的乒乓球(除颜色外其体积、质地完全相同),从袋中随机摸出 个球,
个球,
(1)求摸出的 个球为红球和摸出的
个球为红球和摸出的 个至少一球为黄球的概率分别是多少?
个至少一球为黄球的概率分别是多少?
(2)求摸出的 个球的颜色不相同的概率是多少?
个球的颜色不相同的概率是多少?
(满分12分)假设关于某设备的使用年限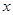 和所支出的维修费用
和所支出的维修费用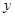 (万元)有如下的统计资料:
(万元)有如下的统计资料:
使用年限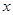 |
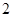 |
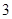 |
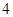 |
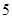 |
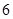 |
维修费用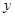 |
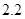 |
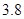 |
 |
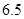 |
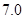 |
若由资料知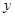 对
对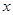 呈线性相关关系。
呈线性相关关系。
(1)请画出上表数据的散点图;
(2)请根据最小二乘法求出线性回归方程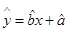 的回归系数
的回归系数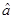 ,
,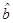 .
.
(3)估计使用年限为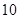 年时,维修费用是多少?
年时,维修费用是多少?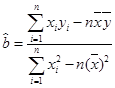 ,
,