高中数学解答题

已知某曲线C的参数方程为，（t为参数，a∈R）点M（5，4）在该曲线上，（1）求常数a；（2）求曲线C的普通方程。

如图，矩形的在变换的作用下分别变成，形成了平行四边形
（1）求变换对应的矩阵；
（2）变换对应的矩阵将直线变成了直线：，求直线的（1）方程.

已知函数.
（1）求的最小正周期；
（2）求在区间上的最大值和最小值.
（3）若g(x)=f(),求函数g(x)的单调增区间；

设集合｛x｝，，
(1)求;          (2)若,求的取值范围。

某沿海地区养殖的一种特色海鲜上市时间仅能持续5个月，预测上市初期和后期会因供不应不足使价格呈持续上涨态势，而中期又将出现供大于求使价格连续下跌．现有三种价格模拟函数：
①；②；③．（以上三式中、均为常数，且）
（1）为准确研究其价格走势，应选哪种价格模拟函数(不必说明理由)
（2）若，，求出所选函数的解析式（注：函数定义域是．其中表示8月1日，表示9月1日，…，以此类推）；
（3）在（2）的条件下研究下面课题：为保证养殖户的经济效益，当地政府计划在价格下跌期间积极拓宽外销，请你预测该海鲜将在哪几个月份内价格下跌．

某校的研究性学习小组为了研究中学生的身高与性别情况，在该校随机抽出80名17至18周岁的学生，其中身高的男生有30人，女生4人；身高<170的男生有10人。
（1）根据以上数据建立一个列联表：

（2）请问在犯错误的概率不超过0.001的前提下，该校17至18周岁的学生的身高与性别是否有关？
参考公式：
参考数据：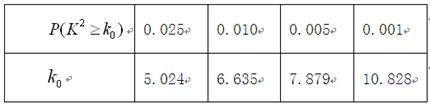

设函数，
（1）求函数的最大值和最小正周期；
（2）设为的三个内角，若，且为锐角，求的值。

设等差数列的前项和为，已知，
（1）求的通项公式；
（2）若，求。

设
（1）求 | z₁| 的值以及z₁的实部的取值范围；
（2）若，求证：为纯虚数.

设复数．
（Ⅰ）若是纯虚数，求实数m的值；
（Ⅱ）若是实数，求实数m的值；
（Ⅲ）若对应的点位于复平面的第二象限，求实数m的取值范围．

（本小题9分）
如图，四棱锥S—ABCD的底面是正方形，SD平面ABCD，SD=2a，，点E是SD上的点，且

（Ⅰ）求证：对任意的，都有
（Ⅱ）设二面角C—AE—D的大小为，直线BE与平面ABCD所成的角为，若，求的值

（本小题8分）
一个口袋内有4个不同的红球，6个不同的白球.
（1）从中任取4个球，红球的个数不比白球少的取法有多少种？
（2）若取一个红球记2分，取一个白球记1分，从中任取4个球，使总分不少于7分的取法有多少种？

为了解某年段1000名学生的百米成绩情况，随机抽取了若干学生的百米成绩，成绩全部介于13秒与18秒之间，将成绩按如下方式分成五组：第一组[13，14）；第二组[14，15）;……;第五组[17，18].按上述分组方法得到的频率分布直方图如图所示，已知图中从左到右的前3个组的频率之比为3∶8∶19，且第二组的频数为8.

（1）将频率当作概率，请估计该年段学生中百米成绩在[16，17）内的人数；
（2）求调查中随机抽取了多少个学生的百米成绩；
（3）若从第一、五组中随机取出两个成绩，求这两个成绩的差的绝对值大于1秒的概率.

已知x＝3是函数f(x)＝alnx＋x²－10x的一个极值点．
(1)求实数a；
(2)求函数f(x)的单调区间．

已知复数，
（1）如果是纯虚数，求实数的值；
（2）设，求复数的值.