高中数学解答题

一个工厂在某年里每月产品的总成本y(万元)与该月产量x(万件)之间有如下组对应数据：

x	1.08	1.12	1.19	1.28	1.36	1.48	1.59	1.68	1.80	1.87	1.98	2.07
y	2.25	2.37	2.40	2.55	2.64	2.75	2.92	3.03	3.14	3.26	3.36	3.50

(1)画出散点图；
(2)求月总成本y与月总产量x之间的回归直线方程．

有人统计了同一个省的6个城市某一年的人均国民生产总值(即人均GDP)和这一年各城市患白血病的儿童数量，如下表：

人均GDP(万元)	10	8	6	4	3	1
患白血病的儿童数	351	312	207	175	132	180

通过计算可得两个变量的回归直线方程为＝23.25x＋102.25，假如一个城市的人均GDP为12万元，那么断言：这个城市患白血病的儿童一定超过380人，请问这个断言是否正确？

已知函数f(x)＝x²＋lnx.
(1)求函数f(x)的单调区间；
(2)求证：当x>1时，x²＋lnx<x³.

有4名男生、5名女生，全体排成一行，问下列情形各有多少种不同的排法？
（1）甲不在中间也不在两端；
（2）甲、乙两人必须排在两端；
（3）男、女生分别排在一起；
（4）男女相间；
（5）甲、乙、丙三人从左到右顺序保持一定．

甲、乙两名篮球运动员互不影响地在同一位置投球，命中率分别为与，且乙投球2次均未命中的概率为。
（1）求乙投球的命中率。
（2）若甲投球1次，乙投球2次，两人共命中的次数记为，求的分布列和数学期望。

有一边长为的正方形铁片，铁片的四角截去四个边长为的小正方形，然后做成一个无盖方盒。

（1）试把方盒的容积表示成的函数；
（2）求多大时，做成方盒的容积最大。

设函数是增函数，函数
在R上有极值，求使命题“p且q”为真的实数m的取值范围。

设计一个算法，求表达式的值，并画出程序框图。

甲、乙两篮球运动员上赛季每场比赛的得分如下：
甲：12,15,24,25,31,31,36,36,37,39,44,49,50；
乙：8,13,14,16,23,26,27,33,38,39,51.
试比较这两位运动员的得分水平．

在直角坐标系中，以坐标原点为极点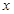，轴的正半轴为极轴建立极坐标系，已知直线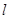的极坐标方程为，曲线的参数方程为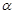（为对数），求曲线截直线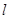所得的弦长.

已知矩阵对应的线性变换把点变成点，求矩阵的特征值以及属于没个特征值的一个特征向量.

在△ABC中，已知，c=1，，求a，A，C．

给出如下For循环语句
S＝0
For i＝1 To 10
S＝S＋i
Next
输出S
(1)写出以上程序语句所执行的算法功能，并求出输出的结果.
(2)试用算法框图表示以上程序语句.

设有120件产品，其中一级品有24件，二级品有36件，三级品有60件，用分层抽样法从中抽取一个容量为20的样本．试说明这种抽样方法是公平的．

某校高一年级500名学生中，血型为O的有200人，血型为A的有125人，B型的有125人，AB型的有50人．为了研究血型与色弱的关系，要从中抽取一个容量为40的样本，应如何抽样？写出AB型的抽样过程．