已知数列 满足:
满足: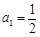 ,
,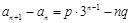 ,
, ,
,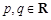 .
.
(1)若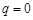 ,且数列
,且数列 为等比数列,求
为等比数列,求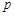 的值;
的值;
(2)若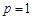 ,且
,且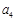 为数列
为数列 的最小项,求
的最小项,求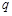 的取值范围.
的取值范围.
设集合 ,记
,记 的含有三个元素的子集个数为
的含有三个元素的子集个数为 ,同时将每一个子集中的三个元素由小到大排列,取出中间的数,所有这些中间的数的和记为
,同时将每一个子集中的三个元素由小到大排列,取出中间的数,所有这些中间的数的和记为 .
.
(1)求 ,
, ,
, ,
, 的值;
的值;
(2)猜想 的表达式,并证明之.
的表达式,并证明之.
(选修4—2:矩阵与变换)
设矩阵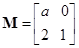 的一个特征值为
的一个特征值为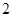 ,若曲线
,若曲线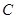 在矩阵
在矩阵 变换下的方程为
变换下的方程为 ,求曲线
,求曲线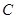 的方程.
的方程.
已知函数 在
在 处的切线方程为
处的切线方程为 .
.
(1)求 的值;
的值;
(2)若对任意的 ,都有
,都有 成立,求
成立,求 的取值范围;
的取值范围;
(3)若函数 的两个零点为
的两个零点为 ,试判断
,试判断 的正负,并说明理由.
的正负,并说明理由.
如图,已知直三棱柱 的侧面
的侧面 是正方形,点
是正方形,点 是侧面
是侧面 的中心,
的中心, ,
, 是棱
是棱 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求证:平面 平面
平面 .
.
如图, 平面
平面

(1)求证:平面 平面
平面 ;
;
(2)求二面角 的大小;
的大小;
(3)求三棱锥 的体积.
的体积.
已知圆C过点A(1,3),B(2,2),并且直线m: 平分圆C的面积.
平分圆C的面积.
(Ⅰ)求圆C的方程;
(Ⅱ)若过点D(0,1)且斜率为k的直线 与圆C有两个不同的公共点M、N,若
与圆C有两个不同的公共点M、N,若 (O为原点),求k的值.
(O为原点),求k的值.
已知函数 的定义域为
的定义域为 .
.
(Ⅰ)若 ,求实数
,求实数 的值;
的值;
(Ⅱ)若 的最小值为5,求实数
的最小值为5,求实数 的值;
的值;
(Ⅲ)是否存在实数 ,使得
,使得 恒成立?若存在求出
恒成立?若存在求出 的值,若不存在请说明理由.
的值,若不存在请说明理由.
如图,三棱柱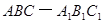 中,
中, 平面ABC,AB
平面ABC,AB BC , 点M , N分别为A1C1与A1B的中点.
BC , 点M , N分别为A1C1与A1B的中点.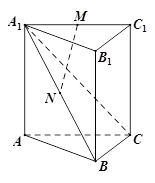
(Ⅰ)求证:MN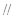 平面BCC1B1;
平面BCC1B1;
(Ⅱ)求证:平面A1BC 平面A1ABB1.
平面A1ABB1.